初中数学一次函数的最值填空题

如图①，在梯形ABCD中，AD∥BC，∠A=60°，动点P从A点出发，以1cm/s的速度沿着A→B→C→D的方向不停移动，直到点P到达点D后才停止．已知△PAD的面积S（单位：cm²）与点P移动的时间（单位：s）的函数如图②所示，则点P从开始移动到停止移动一共用了　      　秒（结果保留根号）．

已知直线（n为正整数）与坐标轴围成的三角形的面积为S_n，则S₁+S₂+S₃+…+S₂₀₁₄=   ．

知实数满足不等式组,且的最小值为,则实数的值是                 ．

矩形A₁B₁C₁O，A₂B₂C₂C₁，A₃B₃C₃C₂，…按如图所示放置．点A₁，A₂，A₃，A₄…和点C₁，C₂，C₃，C₄…，分别在直线 (k＞0)和x轴上，若点B₁(1，2)，B₂(3，4)，且满足,则直线的解析式为                ，点的坐标为               ，点的坐标为_            ．

如图，直线l:，点A₁坐标为(0，1)，过点A₁作y轴的垂线交直线l于点B₁，以原点O 为圆心，OB₁长为半径画弧交y一轴于点A₂；再过点A₂作y轴的垂线交直线于点B₂，以原点O为圆心，OB₂长为半径画弧交y轴于点A₃，…，按此做法进行下去，点A₄的坐标为(_______，_______)；点A_n的坐标为(_______，_______)．

如图，已知直线y=x+4与两坐标轴分别交于A、B两点，⊙C的圆心坐标为 （2，O），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值和最大值分别是　    　．

如图，在平面直角坐标系中，直线l经过原点O，且与x轴正半轴的夹角为30°，点M在x轴上，⊙M半径为2，⊙M与直线l相交于A，B两点，若△ABM为等腰直角三角形，则点M的坐标为　              　．

已知直线y=（n为正整数）与坐标轴围成的三角形的面积为S_n，则S₁+S₂+S₃+…+S₂₀₁₂=           ．

直线y=-2x+m+2和直线y=3x+m-3的交点坐标互为相反数，则m=______。

如图，在平面直角坐标系中直线与轴相交于点A，与反比例函数在第一象限内的图象相交于点B（m，2）．将直线向上平移后与反比例函数图象在第一象限内交于点C，且△ABC的面积为18，求平移后的直线的函数关系式是      ．

如图，平面直角坐标系中，已知直线上一点P（1，1），C为y轴上一点，连接PC，线段PC绕点P顺时针旋转90⁰至线段PD，过点D作直线AB⊥x轴。垂足为B，直线AB与直线交于点A，且BD=2AD，连接CD，直线CD与直线交于点Q，则点Q的坐标为       。

已知点A、B分别在一次函数y=x，y=8x，的图像上，其横坐标分别为a、b(a>0，b>O)．若直线AB为一次函数y=kx+m，的图像，则当是整数时，满足条件的整数k的值共有        个．

如图，已知点A是第一象限内横坐标为的一个定点，AC⊥x轴于点M，交直线y=－x于点N．若点P是线段ON上的一个动点，∠APB=30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是　 　．

如图，一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分）之间的部分关系．那么，从关闭进水管起　   　分钟该容器内的水恰好放完．

钓鱼岛自古就是中国领土，中国政府已对钓鱼岛开展常态化巡逻.某天，为按计划准点到达指定海域，某巡逻艇凌晨1：00出发，匀速行驶一段时间后，因中途出现故障耽搁了一段时间，故障排除后，该艇加快速度仍匀速前进，结果恰好准点到达.如图是该艇行驶的路程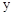（海里）与所用时间t（小时）的函数图象，则该巡逻艇原计划准点到达的时刻是       .