[四川]2014届四川省成都市武侯区九年级上学期期末考试数学试卷
已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是
| A.m≥-1 | B.m≥0 | C.m≥1 | D.m≥2 |
数学老师对小明参加中考前的5次模拟考试进行统计分析,判断小明的数学成绩是否稳定,老师需要知道小明这5次数学成绩的
| A.平均数或中位数 | B.众数或频率 |
| C.方差或极差 | D.频数或众数 |
地球上煤的储量估计仅为15万亿吨,15万亿用科学记数法记为
| A.1.5×1013 | B.0.15×1014 | C.15×1012 | D.1.5×108 |
已知α为锐角,tan(90°-α)= ,则α的度数为
,则α的度数为
| A.30° | B.45° | C.60° | D.75° |
对抛物线 而言,下列结论正确的是
而言,下列结论正确的是
A.与 轴有两个交点 轴有两个交点 |
B.开口向上 |
C.与 轴交点坐标是(0,3) 轴交点坐标是(0,3) |
D.顶点坐标是(1, ) ) |
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=4, CD=1,则EC的长为
A. B.
B. C.
C. D.4
D.4
已知二次函数 中,其函数
中,其函数 与自变量
与自变量 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:
| x |
… |
0 |
1 |
2 |
3 |
4 |
… |
| y |
… |
4 |
1 |
0 |
1 |
4 |
… |
点A( ,
, )、B(
)、B( ,
, )在函数的图象上,则当
)在函数的图象上,则当
 时,
时, 与
与 的大小关系正确的是
的大小关系正确的是
A. B.
B. C.
C.  ≥
≥ D.
D.  ≤
≤
如图,△ABC中,D是AC的中点,E是BC延长线上一点,过A作AH∥BE,连结ED并延长交AB于F,交AH于H,如果AB=4AF,EH=8,则DF的长为 .
小明家所在居民楼的对面有一座大厦AB,AB= 米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
(参考数据: )
)
小丽为了解本市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:

(1)计算被抽取的天数;
(2)请补全条形统计图,并求扇形统计图中表示优的扇形的圆心角度数;
(3)请估计该市这一年(365天)达到优和良的总天数.
如图,已知反比例函数 (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO= (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
(1)若BD是AC边上的中线,如图1,求 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求 的值.
的值.
从-1,0,1,2四个数中选出不同的三个数用作二次函数y=ax2+bx+c的系数,其中不同的二次函数有 个,这些二次函数开口向下且对称轴在y轴的右侧的概率是 .
如图,在平面直角坐标系中直线 与
与 轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线
轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线 向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .
向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .
如图,已知半圆O的直径AB=4,沿它的一条弦折叠.若折叠后的圆弧与直径AB相切于点D,且AD:DB=3:1,则折痕EF的长 .
某服装经营部每天的固定费用为300元,现试销一种成本为每件80元的服装.规定试销期间销售单价不低于成本单价,且获利不得高于35%.经试销发现,每件销售单价相对成本提高x(元)(x为整数)与日均销售量y(件)之间的关系符合一次函数y=kx+b,且当x=10时,y=100;x=20时,y=80.
(1)求一次函数y=kx+b的关系式;
(2)设该服装经营部日均获得毛利润为W元(毛利润=销售收入-成本-固定费用),求W关于x的函数关系式;并求当销售单价定为多少元时,日均毛利润最大,最大日均毛利润是多少元?
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF,OD,OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F= ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
 中自变量x的取值范围是
中自变量x的取值范围是 与
与 在同一坐标系内的图象可以是
在同一坐标系内的图象可以是





 的解集是 .
的解集是 . 有两个相等的实数根,则a的值是 .
有两个相等的实数根,则a的值是 . ,则tanA等于 .
,则tanA等于 .

 ,求
,求 的值.
的值. 的两个不相等的实数根,且满足
的两个不相等的实数根,且满足 ,则m的值是 .
,则m的值是 . 交
交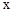 轴于A(2,0),B(6,0)两点,交
轴于A(2,0),B(6,0)两点,交 轴于点C(0,
轴于点C(0, ).
).
 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交 粤公网安备 44130202000953号
粤公网安备 44130202000953号