初中数学一次函数的最值填空题

一次函数y=kx+b的图象如图所示，则不等式0≤kx+b＜5的解集为      ．

一次函数y=2x+b的图象与两坐标轴所围成的三角形的面积为8，则b=       ．

如图，直线y=kx+b与直线y=mx+n交于P（1，），则方程组的解是      ．

若点（m ， n）在函数的图象上，则＝    ．

如图1，长为60km的某段线路AB上有甲、乙两车，分别从南站A和北站B同时出发相向而行，到达B、A后立刻返回到出发站停止，速度均为30km/h，设甲车，乙车距南站A的路程分别为y_甲，y_乙（km）行驶时间为t（h）．
（1）图2已画出y_甲与t的函数图象，其中a＝        ，b＝       ，c＝          ．
（2）分别写出0≤t≤2及2＜t≤4时，y_乙与时间t之间的函数关系式．
（3）在图2中补画y_乙与t之间的函数图象，并观察图象得出在整个行驶过程中两车相遇的次数．
 

如图：直线l₁：y＝k₁x＋b与直线l₂：y＝k₂x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k₁x＋b＞k₂x的解集为           ．

把直线y＝－x－1沿x轴向右平移2个单位,所得直线的函数解析式为        ．

若函数y＝kx－4的图象平行于直线y＝－2x，则函数的表达式是                   ．

已知正比例函数y＝（2m－1）x的图象上两点A（x₁，y₁），B（x₂，y₂），当x₁＜x₂时， 有y₁＞y₂，那么m的取值范围是        ．

图象经过（1，2）的正比例函数的表达式为                     ．

如图， 、分别表示小明步行与小刚骑车在同一条路上行驶的路程S与时间t之间的关系．

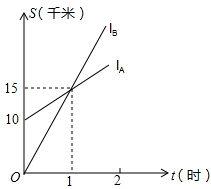
（1）小刚出发时与小明相距      千米．
（2）小刚出发后       小时追上小明．
（3）分别求出小明行走的路程和小刚行走的路程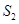与时间t的函数关系式．

画出函数y=-2x+4的图像，根据图像回答下列问题：
（1）y的值随x值的增大而          ；
（2）图像与x轴的交点坐标是       ；图像与y轴的交点坐标是       ；
（3）求图像与两坐标轴围成的三角形的面积．

把直线y=-2x+1向下平移3个单位后得到直线                 ．

已知关于x的函数是一次函数，则m=              ．

如图，直线l₁，l₂交于点A，观察图象，点A的坐标可以看作方程组           的解．