初中数学二次函数在给定区间上的最值试题

抛物线的图象向右移动3个单位，再向下移动4个单位，它的解析式是   

已知二次函数的图象如图所示，对称轴是     ，则下列结论中正确的是（　 　）

Ａ．     Ｂ．  Ｃ Ｄ．

如图，抛物线y＝ax²＋bx＋c的对称轴是x＝，小亮通过观察得出了下面四条信息：①c＜0，②abc＜0，③a－b＋c＞0，④2a－3b＝0。你认为其中正确的有____________________。（填序号）

把二次函数用配方法化成的形式（      ）    

A．

B．

C．

D．

如图，已知抛物线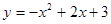与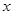轴的两个交点为A、B，与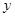轴交于点C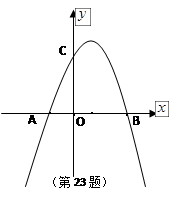

（1）求A、B、C三点的坐标？
（2）用配方法求该二次函数的对称轴和顶点坐标？
（3）若坐标平面内的点M，使得以点M和三点A、B、C为顶点的四边形是平行四边形，求点M的坐标？（直接写出M的坐标，不用说明）

一个二次函数的图象经过点（0，0），（-1，-1），（1，9）三点，求这个函数的关系式

点A是二次函数的图象上的一个点，写出一个
满足条件的A点的坐标是_______

嫦娥二号探月卫星于2010年10月1日发射成功。某科技实验小组也自行设计了火箭，经测试，该种火箭被竖直向上发射时，它的高度h (m)与时间t (s)的关系可以用公式表示．经过______s，火箭达到它的最高点．

已知二次函数的图象经过原点,与x轴的另一个交点为A, 抛物线的顶点为B,则△OAB的面积为    

如图，点A、B的坐标分别为（1, 4）和（4, 4）,一条抛物线与x轴交于C、D两点（C在D的左侧），它的顶点可在线段AB上运动，在运动过程中点C的横坐标最小值为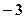，则点D的横坐标最大值为  (    )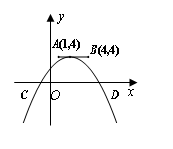

A．－3   　     B．1            C．5            D．8

二次函数的图象如图所示，则一次函数的
图象不经过()

A．第一象限

B．第二象限

C．第三象限

D．第四象限

二次函数的图象可由的图象（）

A．向左平移1个单位，再向下平移2个单位得到

B．向左平移1个单位，再向上平移2个单位得到

C．向右平移1个单位，再向下平移2个单位得到

D．向右平移1个单位，再向上平移2个单位得到

在抛物线上的一个点是（）

A．（4，4）

B．（1，－4）

C．（2，0）

D．（0，4）

下列各式中，y是x的二次函数的是()

A．

B．

C．

D．

(本题12分) 如图，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.

（1）求b,c的值．
（2）连结PO、PC，并把△POC沿CO翻折，得到四边形，那么是否存在点P，使四边形为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时P点的坐标和四边形ABPC的最大面积.