如图,对称轴为x= 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式;
(2)设点E( ,
, )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
图1中的摩天轮可抽象成一个圆,圆上一点离地面的高度y(m)与旋转时间x(min)之间的关系如图2所示
(1)根据图2填表:
| x(min) |
0 |
3 |
6 |
8 |
12 |
… |
| y(m) |
|
|
|
|
|
… |
(2)变量y是x的函数吗?为什么?
(3)根据图中的信息,请写出摩天轮的直径.
如图,在平面直角坐标系中,点 A(5,0),B(3,2),点C在线段OA上,BC=BA,点Q是线段BC上一个动点,点P的坐标是(0,3),直线PQ的解析式为y=kx+b(k≠0),且与x轴交于点D.
(1)求点C的坐标及b的值;
(2)求k的取值范围;
(3)当k为取值范围内的最大整数时,过点B作BE∥x轴,交PQ于点E,若抛物线y=ax2﹣5ax(a≠0)的顶点在四边形ABED的内部,求a的取值范围.
如图,已知抛物线 的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式: (
( ),并指出顶点M的坐标;
),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
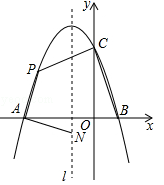
如图,抛物线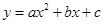 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为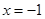 .
.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
如图,在平面直角坐标系中,抛物线 经过A(﹣1,0),B(3,0),C(0,3)三点,其顶点为D.连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
经过A(﹣1,0),B(3,0),C(0,3)三点,其顶点为D.连接BD,点P是线段BD上一个动点(不与B,D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)如果点P的坐标为(x,y),△PBE的面积为S,求S与x的函数关系式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为P′,请求出点P′的坐标.
我们给出如下定义:在平面直角坐标系xOy中,如果一条抛物线平移后得到的抛物线经过原抛物线的顶点,那么这条抛物线叫做原抛物线的过顶抛物线.
如下图,抛物线F2都是抛物线F1的过顶抛物线,设F1的顶点为A,F2的对称轴分别交F1、F2于点D、B,点C是点A关于直线BD的对称点.
(1)如图1,如果抛物线y=x2的过顶抛物线为y=ax2+bx,C(2,0),那么
①a= ,b= .
②如果顺次连接A、B、C、D四点,那么四边形ABCD为( )
A.平行四边形 B.矩形 C.菱形 D.正方形
(2)如图2,抛物线y=ax2+c的过顶抛物线为F2,B(2,c-1).求四边形ABCD的面积.
(3)如果抛物线 的过顶抛物线是F2,四边形ABCD的面积为
的过顶抛物线是F2,四边形ABCD的面积为 ,请直接写出点B的坐标.
,请直接写出点B的坐标.
在平面直角坐标系xOy中,抛物线 经过点A(4,0)和B(0,2).
经过点A(4,0)和B(0,2).
(1)求该抛物线的表达式;
(2)在(1)的条件下,如果该抛物线的顶点为C,点B关于抛物线对称轴对称的点为D,求直线CD的表达式;
(3)在(2)的条件下,记该抛物线在点A,B之间的部分(含点A,B)为图象G,如果图象G向上平移m(m>0)个单位后与直线CD只有一个公共点,请结合函数的图象,直接写出m的取值范围.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点. 
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=ax2+bx+c的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(- ,0),以0C为直径作半圆,圆心为D.
,0),以0C为直径作半圆,圆心为D.
(1)求二次函数的解析式;
(2)求证:直线BE是⊙D的切线;
(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.
(本题8分)某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要赢利1200元,且让顾客得到实惠,每件衬衫应降价多少元?
(2)要使商场平均每天赢利最多,则每件衬衫应降价多少元?
如图,抛物线 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
(1)填空:点C的坐标为( , ),点D的坐标为( , );
(2)设点P的坐标为(a,0),当 最大时,求a的值并在图中标出点P的位置;
最大时,求a的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
抛物线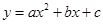 ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线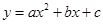 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线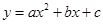 必过x轴上的一个定点A;
必过x轴上的一个定点A;
(2)已知“恒定”抛物线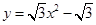 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a= .
.
①求点D的坐标及该抛物线的解析式.
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由.
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余,若符合条件的Q点的个数是4个,请直接写出a的取值范围.
如图,抛物线 与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
(1)求抛物线的解析式;
(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
①当四边形OMHN为矩形时,求点H的坐标;
②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.