二次函数y=ax2+bx+c的图像如图所示,则①abc;②b2-4ac;③2a+b;④a+b+c这四个式子中,值为负数的有个
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F,设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )

抛物线y=-x2+2x-2经过平移得到y=-x2,平移方法是( )
| A.向右平移1个单位,再向下平移1个单位 |
| B.向右平移1个单位,再向上平移1个单位 |
| C.向左平移1个单位,再向下平移1个单位 |
| D.向左平移1个单位,再向上平移1个单位 |
如图,抛物线y=-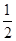 x2+
x2+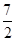 x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
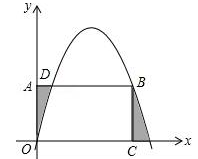
A.3 B.4 C.5 D.6
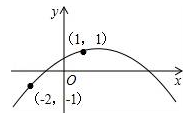
如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是( )
| A.y的最大值小于0 |
| B.当x=0时,y的值大于1 |
| C.当x=-1时,y的值大于1 |
| D.当x=-3时,y的值小于0 |
将抛物线y=x2-4x+5的顶点A向左平移2个单位长度得到点 ,则点
,则点 的坐标是( )
的坐标是( )
| A.(2,3) | B.(2,-1) | C.(4,1) | D.(0,1) |
如图,抛物线 与矩形OABC的AB边交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
与矩形OABC的AB边交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )

A.3 B.4 C.5 D.6
如图,二次函数的图像经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是( )

| A.y的最大值小于0 |
| B.当x=0时,y的值大于1 |
| C.当x=-1时,y的值大于1 |
| D.当x=-3时,y的值小于0 |
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为

若二次函数 的
的 与
与 的部分对应值如下表:
的部分对应值如下表:
 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
| y |
-27 |
-13 |
-3 |
3 |
5 |
3 |
则当 时,
时, 的值为( )
的值为( )
A.5 B.-3 C.-13 D.-27
已知二次函数y=2(x﹣3)2+1,下列说法:
①其图象的开口向下;
②其图象的对称轴为直线x=﹣3;
③其图象顶点坐标为(3,﹣1);
④当x<3时,y随x的增大而减小.
则其中说法正确的有
| A.1个 | B.2个 | C.3个 | D.4个 |