初中数学二次函数在给定区间上的最值试题

若将二次函数y = x²- 2x + 3配方为y = （ x - h ）² + k的形式，则y = ________．

抛物线与轴只有一个公共点，则的值为         ．

函数和在同一直角坐标系中图象可能是图中的                             

抛物线y =x²向左平移8个单位，再向下平移9个单位后，所得抛物线的表达式是

A．y=（x+8）^2-9	B．y=（x-8）^2+9
C．y=（x-8）^2-9	D．y=（x+8）^2+9

对于抛物线下列说法正确的是

A．开口向下，顶点坐标

B．开口向上，顶点坐标

C．开口向下，顶点坐标

D．开口向上，顶点坐标

某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本＝每件的成本×每天的销售量）

二次函数y＝2x²＋bx＋c的图象经过点（2，1），（0，1）．
（1）求该二次函数的表达式及函数图象的顶点坐标和对称轴；
（2）若点P），Q）在抛物线上，试判断y1与y2的大小．（写出判断的理由）

如果将抛物线y=x²向右平移1个单位，那么所得的抛物线的表达式是（ ）

A．y=x^2-1

B．y=x^2+1

C．y=（x-1）^2

D．y=（x+1）^2

二次函数的图象与轴有交点，则的取值范围是（  ）

A．

B．

C．

D．

抛物线的部分图像如图所示，若y>0，则的取值范围是（  ）

A．-4＜x＜1	B．
C．	D．

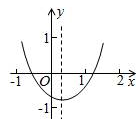
已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a-b+c＜0；③b+2a＜0；④abc＞0，其中所有正确结论的序号是             ．

如果函数y=（k-3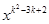）+kx+1是二次函数，那么k的值一定是          ．

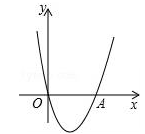
若二次函数y=ax²+bx+a²-2（a，b为常数）的图象如下，则a的值为（ ）

A．-2

B．-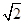

C．1

D．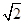

某商场购进一批L型服装（数量足够多），进价为40元/件，以60元/件销售，每天销售20件，根据市场调研，若每件降价1元，则每天销售数量比原来多3件．现商场决定对L型服装开展降价促销活动，每件降价x元（x为正整数）．在促销期间，商场要想每天获得最大销售毛利润，每件应降价多少元？每天最大销售毛利润为多少？（注：每件服装销售毛利润是指每件服装的销售价与进货价的差）

抛物线y=x²+2x+3的顶点坐标是              ．