已知抛物线 y=ax2+bx+3 (a≠0) 经过A(5,0), B(6,1)两点,且与y轴交于点C.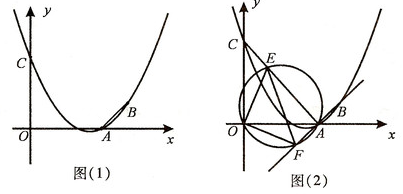
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A重合)经过A、E、O三点的圆交直线AB于点F,求出当△OEF的面积取得最小值时,点E的坐标.
在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是 ,当水位上涨1m时,水面宽CD为
,当水位上涨1m时,水面宽CD为 m,则桥下水面宽AB为____________m
m,则桥下水面宽AB为____________m 
抛物线y=x2+2x-1关于y轴对称的抛物线的解析式为 ( )
| A.y=x2-2x-1 | B.y=x2-2x-3 |
| C.y=-x2+2x-3 | D.y=-x2-2x-1 |
二次函数y=a +bx+c(a≠0)的图象如图所示,下列结论正确的是( )
+bx+c(a≠0)的图象如图所示,下列结论正确的是( )

| A.a<0 |
B. -4ac<0 -4ac<0 |
| C.当-1<x<3时,y>0 |
D.- =1 =1 |
把抛物线y=-x2向左平移1个单位长度,然后向上平移3个单位长度,则平移后抛物线的解析式为( )
| A.y=-(x-1)²-3 |
| B.y=-(x+1)²-3 |
| C.y=-(x-1)²+3 |
| D.y=-(x+1)²+3 |
如图,已知抛物线y=-ax2+2ax+3a(a≠0)与x轴交于A、B两点,与y轴交于点C.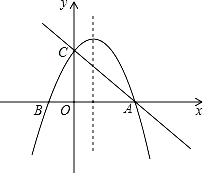
(1)请直接写出A、B两点的坐标.
(2)当a=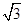 ,设直线AC与抛物线的对称轴交于点P,请求出△ABP的面积.
,设直线AC与抛物线的对称轴交于点P,请求出△ABP的面积.
对于抛物线y=ax2+bx+c(a≠0),有下列说法:
①当b=a+c时,则抛物线y=ax2+bx+c一定经过一个定点(-1,0);
②若△=b2-4ac>0,则抛物线y=cx2+bx+a与x轴必有两个不同的交点;
③若b=2a+3c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
④若a>0,b>a+c,则抛物线y=ax2+bx+c与x轴必有两个不同的交点;
其中正确的有 .
已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
| x |
… |
0 |
1 |
2 |
3 |
… |
| y |
… |
5 |
2 |
1 |
2 |
… |
点A(x1,y1)、B(x2,y2)在函数的图象上,则当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
A.y1≥y2 B.y1>y2 C.y1<y2 D.y1≤y2
如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是( )
| A.y=x2-1 | B.y=x2+6x+5 | C.y=x2+4x+4 | D.y=x2+8x+17 |
将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
| A.y=(x﹣1)2+2 |
| B.y=(x+1)2+2 |
| C.y=(x﹣1)2﹣2 |
| D.y=(x+1)2﹣2 |
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=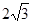 ,直线
,直线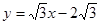 经过点C,交y轴于点G.
经过点C,交y轴于点G.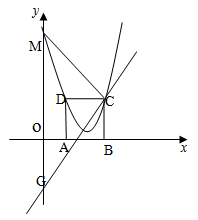
(1)求C,D坐标;
(2)已知抛物线顶点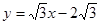 上,且经过C,D,若抛物线与y交于点M连接MC,设点Q是线段下方此抛物线上一点,当点Q运动到什么位置时,△MCQ的面积最大?求出此时点Q的坐标和面积的最大值.
上,且经过C,D,若抛物线与y交于点M连接MC,设点Q是线段下方此抛物线上一点,当点Q运动到什么位置时,△MCQ的面积最大?求出此时点Q的坐标和面积的最大值.
(3)将(2)中抛物线沿直线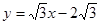 平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求 出此时抛物线的解析式;若不存在,请说明理由.
平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求 出此时抛物线的解析式;若不存在,请说明理由.