实践应用（本小题满分6分）
有200名待业人员参加某企业甲、乙、丙三个部门的招聘，到各部门报名的人数百分比见图表1，该企业各部门的录取率见图表2.（部门录取率=
×100%）
（1）到乙部门报名的人数有 人，乙部门的录取人数是 人，该企业的录取率为 ；
（2）如果到甲部门报名的人员中有一些人员改到丙部门报名，在保持各部门录取率不变的情况下，该企业的录取率将恰好增加15%，问有多少人从甲部门改到丙部门报名？
小明新买了一辆“和谐”牌自行车，说明书中关于轮胎的使用说明如下：
小明看了说明书后，和爸爸讨论：小明经过计算，得出这对轮胎能行驶的最长路程是（ ）
| A．9.5千公里 | B． 千公里 |
C．9.9千公里 | D．10千公里 |
（本小题满分10分）
问题再现
现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.
我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如图，用正方形镶嵌平面，可以发现在一个顶点O周围围绕着4个正方形的内角.
试想：如果用正六边形镶嵌平面，在一个顶点周围应该围绕 个正六边形内角．
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？
问题解决
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？
分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意，可得方程：
，整理得：
，
我们可以找到惟一一组适合方程的正整数解为
．
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．
上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．
问题拓广
请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．
将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图6-1．在图6-2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．若骰子的初始位置为图6-1所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是
| A．6 | B．5 | C．3 | D．2 |
为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两间工厂了解情况，获得如下信息：
信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；
信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品？
一天，小青在校园内发现：旁边一颗树在阳光下的影子和她本人的影子在同一直线上，树顶的影子和她头顶的影子恰好落在地面的同一点，同时还发现她站立于树影的中点（如图所示）.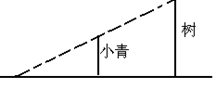
如果小青的峰高为1.65米，由此可推断出树高是_______米.
从小明家到学校的路程是2400米，如果小明早上7点离家，要在7点30分到40分之间到达学校，设步行速度为
米/分，小明步行的速度范围是_________。
在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后返回．设汽车从甲地出发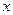
（h）时，汽车与甲地的距离为
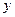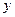（km），与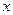的函数关系如图所示．
根据图象信息，解答下列问题：
（1）这辆汽车的往、返速度是否相同？请说明理由；
（2）求返程中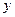与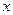之间的函数表达式；
（3）求这辆汽车从甲地出发4h时与甲地的距离．
小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：
如示意图，小明边移动边观察，发现站到点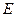
处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度
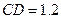m，
m，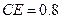
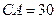m（点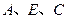
在同一直线上）．
已知小明的身高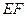
是1.7m，请你帮小明求出楼高
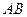（结果精确到0.1m）．
一家商店将某种商品按成本价提高50%后，标价为450元，又以8折出售，则售出这件商品可获利润__________元．
某单位需以“挂号信”或“特殊快递”的方式向五所学校各寄一封信.这五封信的质量分别是90g，72g，215g，340g，400g. 根据这五所学校的地址及信件的质量范围，在邮局查得相关邮费标准如下：
| 业务种类 |
计费单位 |
资费标准 （元） |
挂号费 （元/封） |
特制信封 （元/个） |
| 挂号信 |
首重100g内，每20g |
0.8 |
3.0 |
0.5 |
| 续重101g—2000g 每100g |
2.0 |
|||
| 特快专递 |
首重1000g （含1000g） |
5.0 |
3.0 |
1.0 |
|
作图题：
（1）如图，有两个7×4的网格，网格中每个小正方形的边长均为1，每个网格中各画有一个梯形。请在图①、图②中分别画出一条线段，同时满足以下要求：
①线段的一个端点为梯形的顶点，另一个端点在梯形一边的格点上；
②将梯形分成两个图形，其中一个是轴对称图形；
③图①、图②中分成的轴对称图形不全等。
（2）近年来，国家实施“村村通”工程和农村医疗卫生改革，某县计划在张村、李村之间建一座定点医疗站
，张、李两村座落在两相交公路内(如图所示)．医疗站必须满足下列条件：①使其到两公路距离相等，②到张、李两村的距离也相等，请你通过作图确定点的位置．
依法纳税是公民应有的义务，《个人所得税法》规定，每月总收入减去2000元后的余额为应纳税所得额，应纳税所得额不超过500元的部分按5%纳税；超过500元但不超过2000元的部分按10%纳税，若职工小李某月税前总收入3200元，则该月他应纳税_______元．
小王利用计算机设计了一个计算程序，输入和输出的数据如下表：
| 输入 |
…… |
1 |
2 |
3 |
4 |
5 |
…… |
| 输出 |
…… |
 |
 |
 |
 |
 |
…… |
那么当输入数据是8时，输出的数据是_____________．
粤公网安备 44130202000953号