(本题4分)把下列各数分别填入相应的集合内:
-2.5,0,8,-2, ,
, ,-0.5252252225…(每两加1个2).
,-0.5252252225…(每两加1个2).
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)无理数集合:{ …}.
如图,数轴上A、B两点分别对应实数a、b,则下列结论正确的是
A. B.
B.
C. D.
D.
下列说法正确的是( )
| A.倒数等于它本身的数只有1 |
| B.任何数的开方都是正数 |
| C.绝对值等于它本身的数只有0 |
| D.相反数等于它本身的数只有0 |
下列说法不正确的是( )
| A.0既不是正数,也不是负数 |
| B.互为相反数的两个数的和为0 |
| C.互为倒数的两个数的和为1 |
| D.0的绝对值是0 |
用“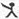 ”、“
”、“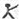 ”定义新运算:对于任意实数a,b,都有a
”定义新运算:对于任意实数a,b,都有a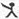 b=a和a
b=a和a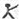 b=b,例如3
b=b,例如3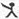 2=3,3
2=3,3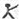 2=2。则(2013
2=2。则(2013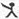 2014)
2014) 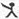 (2011
(2011 2012)的值是
2012)的值是
(1)如图,圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.小明从编号为4的点开始,第三次“移位”后,他到达编号为 的点,第2012次“移位”后,他到达编号为 的点.
(2)若将圆进行二十等份,按照顺时针方向依次编号为1,2,3,…,20,小明从编号为3的点开始,沿顺时针方向,按上述“移位”方式行走,
①经过4次“移位”后,他到达编号为 的点.
②“移位”次数a= 时,小王刚好到达编号为16的点,又满足|a-2012|的值最小.
把几个数用大括号围起来,中间用逗号断开,如:{1,2,-3}、{−2,7,3 ,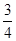 ,19},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数10-a也必是这个集合的元素,这样的集合我们称为和谐集合.例如集合{2,8},{-1,
,19},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数10-a也必是这个集合的元素,这样的集合我们称为和谐集合.例如集合{2,8},{-1,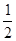 ,
,  ,11}就是两个和谐集合.
,11}就是两个和谐集合.
(1)请你判断集合{1,-10},{-2,3.14,5,6.86,12}是不是和谐集合?
(2)请你写出满足条件的两个和谐集合的例子(至少有3个元素且不能与例题举例重复);
(3)写出所有和谐集合中,元素个数最少的集合.
用“☆”“★”定义新运算;对于任意实数a、b,都有a☆b=a和a★b=b.例如5☆2=5,2★4=4,则2014☆(2014★2015)=_______。
下列说法:①如果两个数的积为1,则这两个数互为倒数;②如果两个数和为0,则至少有一个数为0;③绝对值是本身的有理数只有1;④倒数是本身的数是-1,0,1。⑤零有相反数。其中错误的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是.(填写所有正确结论的序号)
①[0)=0②[x)-x的最小值是0③[x)-x的最大值是0④存在实数x,使[x)-x=0.5成立.
某初中校为每个学生编号,设定末尾用1表示男生,用2表示女生,若201103202表示“2011年入学的3班20号同学,是位女生”,则2012年入学的5班13号男生的编号是 .