初中数学有理数无理数的概念与运算试题

若|2x|= -2x，则x一定是（  ）

A．正数

B．负数

C．正数或0

D．负数或0

由图可知，a、b、c的大小关系为（   ）

A．a < b < c

B．a < c < b

C．c < a < b

D．c < b < a

已知有理数a ，b在数轴上表示的点如图所示，则下列式子中不正确的是（    ）

A．	B．
C．	D．

将图1中的正方形剪开得到图2，图2中共有4个正方形；将图2中一个正方形剪开得到图3，图3中共有7个正方形；将图3中一个正方形剪开得到图4，图4中共有10个正方形；……；如此下去．则图10中正方形的个数是（   ）

A．28

B．29

C．31

D．32

宁宁同学设计了一个计算程序，如下表

输入数据	1	2	3	4	5
输出数据					a

根据表格中的数据的对应关系，可得a的值是________

猜数字游戏中，小明写出如下一组数：…，小亮猜想出第六个数字是，根据此规律，第n个数是　       　．

有理数a、b在数轴上的位置如图所示，则a＋b的值（    ）

A．大于0

B．小于0

C．小于a

D．大于b

在迎新春活动中，三位同学玩抢2013游戏，甲、乙、丙围成一圈依序报数，规定：甲、乙、丙首次报的数依次为1、2、3、，接着甲报4、乙报5……按此规律，后一位同学报的数比前一位同学报的数大1，当报的数是2013时，报数结束；按此规则，最后能抢到2013的同学是          ．

探索规律：货物箱按如图方式堆放（自下而上依次为第1层、第2层、…），受堆放条件限制，堆放时应符合下列条件：每层堆放货物箱的个数与层数n之间满足关系式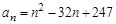，为正整数.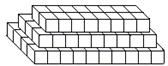

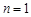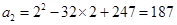例如，当时，, 当时，，则：
＝           ，＝            ；
⑵ 第n层比第（n＋1）层多堆放           个货物箱.（用含n的代数式表示）

我们把大于1的正整数m的三次幂按一定规则“分裂”成若干个连续奇数的和，如2³＝3＋5，
3³＝7＋9＋11，4³＝13＋15＋17＋19，……，若m³按此规则“分裂”后，其中有一个奇数是313，则m的值是（    ）

A．20

B．19

C．18

D．17

下列说法中不正确的是 (      )

A．－1的倒数是－1	B．－1的立方根是－1
C．－π＜－3.14	D．用四舍五入法将16.47取近似值精确到个位是17

如右图，连接在一起的两个正方形的边长都为1cm，一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动．当微型机器人移动了2013cm时，它停在          点．

有理数数、在数轴上的位置如图所示，则化简的结果为（ 　 ）

A．

B．

C．

D．

如图，在某高速公路上从3千米处开始，每隔4千米设置一个速度限制标志，而且从10千米处开始，每隔9千米设置一个测速照相机标志，则刚好在19千米处同时设置这两种标志.那么下一个同时设置这两种标志的地点的千米数是_______.

这是一根起点为0的数轴，现有同学将它弯折，如图所示，例如：虚线上第一行0，第二行6，第三行21，……，第10行的数是（    ）

A．351

B．702

C．378

D．756