[浙江]2013学年浙江省杭州市拱墅区第一学期期末教学质量调研七年级数学试卷
地球半径约为6 400 000米,用科学记数法表示为( )
| A.0.64×107 | B.6.4×106 | C.64×105 | D.6×106 |
一个正方形的面积是9平方单位,则这个正方形的边长是( )长度单位
| A.3 | B. |
C.± |
D.± |
如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度后,再向左移动2个单位长度得到点P′,则点P′表示的数是( )
| A.3 | B.2 | C.1 | D.0 |
下列说法中不正确的是 ( )
| A.-1的倒数是-1 | B.-1的立方根是-1 |
| C.-π<-3.14 | D.用四舍五入法将16.47取近似值精确到个位是17 |
如图,点C到直线AB的距离是指哪条线段长( )
| A.CB | B.CD | C.CA | D.DE |
若| m-1 |+| n-3 |=0,则(m-n)3的值为( )
| A.6 | B.-6 | C.8 | D.-8 |
某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,如果要使得利润率为5%,那么销售时应该打( )
| A.6折 | B.7折 | C.8折 | D.9折 |
如果点C在线段AB上,下列表达式:①AC= AB; ②AB=2BC; ③AC=BC; ④AC+BC=AB中, 能表示点C是线段AB中点的有( )
AB; ②AB=2BC; ③AC=BC; ④AC+BC=AB中, 能表示点C是线段AB中点的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
洪峰到来前,120名战士奉命加固堤坝,已知3人运送沙袋2人堆垒沙袋,正好运来的沙袋能及时用上且不窝工. 为了合理安排,如果设x人运送沙袋,其余人堆垒沙袋,那么以下所列方程正确的是( )
A. |
B. |
C. |
D.2x+3x=120 |
我们把大于1的正整数m的三次幂按一定规则“分裂”成若干个连续奇数的和,如23=3+5,
33=7+9+11,43=13+15+17+19,……,若m3按此规则“分裂”后,其中有一个奇数是313,则m的值是( )
| A.20 | B.19 | C.18 | D.17 |
某企业为贫困山区孩子送温暖,共捐出衣物和棉被共1800件,已知衣物的件数比棉被件数的3倍少200件,则该企业捐的棉被有 件.
画一个∠AOB,使∠AOB=30°,再作OC⊥OA,OD⊥OB,则∠COD的度数是 .
探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数 与层数n之间满足关系式
与层数n之间满足关系式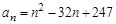 ,
, 为正整数.
为正整数. 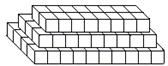
例如,当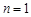 时,
时, , 当
, 当 时,
时,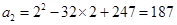 ,则:
,则: = ,
= , = ;
= ;
⑵ 第n层比第(n+1)层多堆放 个货物箱.(用含n的代数式表示)
计算
(1)-1+2×3 ;(2) ; (3)
; (3) ;(4)90°-45°58/ ; (5) 38°36/ +72.5°(结果用度表示)
;(4)90°-45°58/ ; (5) 38°36/ +72.5°(结果用度表示)
作图与回答:
(1)已知线段a和b, 请用直尺和圆规作出线段AB,使AB=2a―b.(不必写作法,只需保留作图痕迹)
(2)已知直线AB与CD垂直,垂足为O,请在图中用量角器画射线OE表示北偏西30°、画射线OF表示南偏东30°、画射线OH表示北偏东45°.
(3)找一找,你完成的作图(2)中是锐角的对顶角有几组,
把它们写出来.
(1)已知一个角的余角是这个角的补角的 ,求出这个角以及这个角的余角和补角.
,求出这个角以及这个角的余角和补角.
(2)如图21-(2),已知直线AB和CD相交于O点,CO⊥OE, OF 平分∠AOE, ∠COF=26°, 求∠BOD的度数.
化简与求值:
(1)当 时,求代数式
时,求代数式 的值;
的值;
(2)当 时,求代数式
时,求代数式 的值;
的值;
(3)求整式 与
与 的和,并说明当
的和,并说明当 、
、 均为无理数时,结果是一个什么数?
均为无理数时,结果是一个什么数?
如图,是舟山--嘉兴的高速公路示意图,王老师驾轿车从舟山出发,上高速公路途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了20千米/小时,比去时少用了1小时回到舟山.
(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见下表: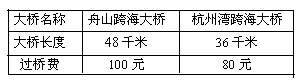
我省交通部门规定:轿车的高速公路通行费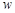 (元)的计算方法为:
(元)的计算方法为: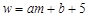 ,其中a元/(千米)为高速公路里程费,
,其中a元/(千米)为高速公路里程费,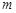 (千米)为高速公路里程数(不包括跨海大桥长),
(千米)为高速公路里程数(不包括跨海大桥长),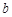 (元)为跨海大桥过桥费.若王老师从舟山到嘉兴所花的高速公路通行费为277.4元,求轿车的高速公路里程费
(元)为跨海大桥过桥费.若王老师从舟山到嘉兴所花的高速公路通行费为277.4元,求轿车的高速公路里程费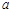 .
.
 ,
, ,
, ,π,
,π, 中,最大的数是 ;有理数有 个.
中,最大的数是 ;有理数有 个. ,则
,则 = .
= . 与
与 是同类项、
是同类项、 的系数为
的系数为 、
、 的次数是4:先分别求出x、y、m,然后计算
的次数是4:先分别求出x、y、m,然后计算 的值
的值 -1.
-1. 粤公网安备 44130202000953号
粤公网安备 44130202000953号