初中数学列表法与树状图法填空题

在不透明的甲、乙两个盒子中装有除颜色外完全相同的小球，甲盒中有2个白球、1个黄球，乙盒中有1个白球、1个黄球，分别从每个盒中随机摸出1个球，则摸出的2个球都是黄球的概率是　　．

同时抛掷两枚质地均匀的硬币，一枚硬币正面向上，一枚硬币反面向上的概率是　　．

同时抛掷两枚质地均匀的硬币，则两枚硬币全部正面向上的概率是　　．

有两个不透明的盒子，第一个盒子中有3张卡片，上面的数字分别为1，2，2；第二个盒子中有5张卡片，上面的数字分别为1，2，2，3，3．这些卡片除了数字不同外，其它都相同，从每个盒子中各抽出一张，都抽到卡片数字是2的概率为　   　．

若从 $-1$，1，2这三个数中，任取两个分别作为点 $M$的横、纵坐标，则点 $M$在第二象限的概率是　　．

淘淘和丽丽是非常要好的九年级学生，在5月份进行的物理、化学、生物实验技能考试中，考试科目要求三选一，并且采取抽签方式取得，那么他们两人都抽到物理实验的概率是　　．

如图，随机地闭合开关 $S_1$， $S_2$， $S_3$， $S_4$， $S_5$中的三个，能够使灯泡 $L_1$， $L_2$同时发光的概率是　         　．

2018年5月18日，益阳新建西流湾大桥竣工通车，如图，从沅江 $A$地到资阳 $B$地有两条路线可走，从资阳 $B$地到益阳火车站可经会龙山大桥或西流湾大桥或龙洲大桥到达，现让你随机选择一条从沅江 $A$地出发经过资阳 $B$地到达益阳火车站的行走路线，那么恰好选到经过西流湾大桥的路线的概率是　　．

从2018年高中一年级学生开始，湖南省全面启动高考综合改革，学生学习完必修课程后，可以根据高校相关专业的选课要求和自身兴趣、志向、优势，从思想政治、历史、地理、物理、化学、生物6个科目中，自主选择3个科目参加等级考试．学生 $A$已选物理，还从思想政治、历史、地理3个文科科目中选1科，再从化学、生物2个理科科目中选1科．若他选思想政治、历史、地理的可能性相等，选化学、生物的可能性相等，则选修地理和生物的概率为　　．

掷两枚质地均匀的相同硬币，出现两枚都是正面朝上的概率为　　．

掷一枚硬币两次，可能出现的结果有四种，我们可以利用如图所示的树状图来分析所有可能出现的结果，那么掷一枚硬币两次，至少有一次出现正面的概率是　　．

在如图所示的电路中，随机闭合开关 $S_1$， $S_2$， $S_3$中的两个，能让灯泡 $L_1$发光的概率是　　．

从1、 $-1$、0三个数中任取两个不同的数作为点的坐标，则该点在坐标轴上的概率是　　．

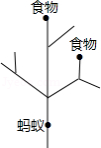
一只昆虫在如图所示的树枝上寻觅食物，假定昆虫在每个岔路口都会随机选择一条路径，则它获取食物的概率是　　．

从 $-1$，0，1，2这四个数中，任取两个不同的数作为点的坐标，则该点在第一象限的概率为　　．