初中数学相似多边形的性质填空题

如图，在平面直角坐标系中，四边形OABC是边长为4的正方形，M（4，m）、N（n，4）分别是AB、BC上的两个动点，且ON⊥MN，当OM最小时，＝    ．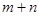

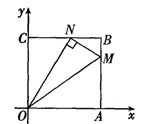
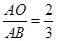如图，双曲线经过Rt△BOC斜边上的点A，且满足，与BC交于点D，S_△BOD=21，求k= _________ ．

如图，在直线m上摆放着三个正三角形：△ABC、△HFG、△DCE，已知BC=CE，F、G分别是BC、CE的中点，FM∥AC，GE∥DC、设图中三个平行四边形的面积依次是、、，若，则=      ．

如图，在边长为6的正方形ABCD中，动点M从点A出发，沿A→B→C向终点C运动，连接DM交AC于点N，若点M运动所经过的路程为x（6≤x≤12），那么当△ADN为等腰三角形时，x的值为___________。

如图，在正方形ABCD中，点P是AB上一动点（不与A、B重合），对角线AC，BD相交于点O，过点P分别作AC，BD的垂线，分别交AC，BD于点E，F，交AD，BC于点M，N．下列结论：①△APE≌△AME；
②PM+PN=AC；
③PE²+PF²=PO²；
④△POF∽△BNF；
⑤当△PMN∽△AMP时，点P是AB的中点．
其中正确的结论是           ．

在△ABC中，AB=6cm，AC=5cm，点D、E分别在AB、AC上．若△ADE与△ABC相似，且S_△ADE：S_{四边形BCED}=1：8，则AD=     cm．

如图，平行四边形ABCD中，AB=5，AD=7，AB⊥AC，点E在边AD上，满足=，点F在AB上，满足 =，连结BE和CF相交于点G，则线段CG的长度是     ．

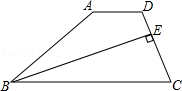
如图，在梯形ABCD中，AD∥BC，BE平分∠ABC交CD于E，且BE⊥CD，CE:ED=2:1．如果△BEC的面积为2，那么四边形ABED的面积是         ．

如图，△ABC是一张直角三角形彩色纸，AC=15cm，BC=20cm．若将斜边上的高CD 分成n等分，然后裁出（n﹣1）张宽度相等的长方形纸条．则这（n﹣1）张纸条的面积和是   cm²．

将一副三角尺如图所示叠放在一起，则               ．

如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使得两个直角的顶点重合于对角线BD上一点P，EF、GH分别是折痕（如图2）．设AE＝x（0＜x＜2），给出下列判断：

①当x＝1时，点P是正方形ABCD的中心；
②当x＝时，EF＋GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的是________（填序号）．

如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ=CE时，EP+BP=            ．

AD为△ABC的中线，G为△ABC的重心，若=2，则=      ．

如图，在△ABC中，E，F分别是AC，BC边上的点，P₁，P₂，P₃，…，P_n−1是AB边的n等分点，CE = AC，CF = BC，∠B = 40°，AB = BC，则∠EP₁F +∠EP₂F +∠EP₃F + … +∠EP _n−1F = ________．

点A,B,C都在半径为r的圆上，直线AD⊥直线BC，垂足为D，直线BE⊥直线AC，垂足为E，直线AD与BE相交于点H，若，则∠ABC所对的弧长等于       （长度单位）.