如图,已知△ABC中,AB=5,AC=3,点D在边AB上,且∠ACD=∠B,则线段AD的长为 .
如图,在△ABC中,E,F分别为AB,AC的中点,则△AEF与△ABC的面积之比为 .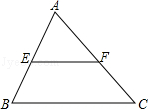
如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是 米(平面镜的厚度忽略不计).
如图,在△ABC中,若DE∥BC, ,且S△ADE=4cm2,则四边形BCED的面积为 .
,且S△ADE=4cm2,则四边形BCED的面积为 .
为了测量水塔的高度,我们取一竹竿,放在阳光下,已知2米长的竹竿投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为 米.
如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则网球的击球的高度h为 .
如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,...,按此规律继续下去,则矩形ABnCnCn-1的面积为 .
如图,已知△ABC的三边长为 、
、 、
、 ,且
,且 ,若平行于三角形一边的直线
,若平行于三角形一边的直线 将△ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为
将△ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为 、
、 、
、 则
则 、
、 、
、 的大小关系是 (用“<”号连接).
的大小关系是 (用“<”号连接).
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上,若线段AB="4" cm,则线段BC= cm
如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=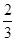 EH,那么EH的长为 .
EH,那么EH的长为 .
如图,∠ACB=∠ADC=90°,AC=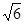 ,AD=2,当AB的长为 时,△ACB与△ADC相似.
,AD=2,当AB的长为 时,△ACB与△ADC相似.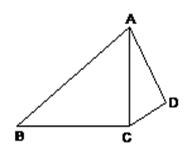
如图,∠1=∠2,添加一个条件,使得 ∽
∽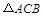 .你添加的条件是: .
.你添加的条件是: .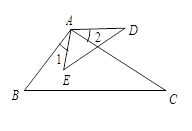
如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、Pn,把△ABC分成 个互不重叠的小三角形.