2015年初中毕业升学考试(江苏扬州卷)数学
2015年我国大学生毕业人数将达到7490000人,这个数据用科学记数法表示为( )
A.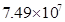 |
B.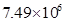 |
C.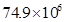 |
D.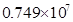 |
如图是某校学生参加课外兴趣小组的人数占总人数比例的 统计图,则参加人数最多的课外兴趣小组是 ( )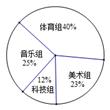
| A.音乐组 | B.美术组 | C.体育组 | D.科技组 |
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC 经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种 变换可以是 ( )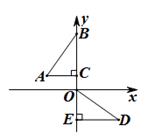
A、△ABC绕点C顺时针旋转90°,再向下平移3
B、△ABC绕点C顺时针旋转90°,再向下平移1
C、△ABC绕点C逆时针旋转90°,再向下平移1
D、△ABC绕点C逆时针旋转90°,再向下平移3
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论: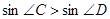 ;
;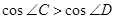 ;
;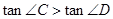 中,正确的结论为( )
中,正确的结论为( )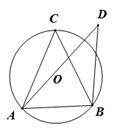
| A. | B. | C. | D. |
已知x=2是不等式 ≤0的解,且x=1不是这个不等式的解,则实数
≤0的解,且x=1不是这个不等式的解,则实数 的取值范围是( )
的取值范围是( )
A. |
B. ≤2 ≤2 |
C. ≤2 ≤2 |
D.1≤ ≤2 ≤2 |
色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如下表:
| 抽取的体检表数n |
50 |
100 |
200 |
400 |
500 |
800 |
1000 |
1200 |
1500 |
2000 |
| 色盲患者的频数m |
3 |
7 |
13 |
29 |
37 |
55 |
69 |
85 |
105 |
138 |
| 色盲患者的频率m/n |
0.060 |
0.070 |
0.065 |
0.073 |
0.074 |
0.069 |
0.069 |
0.071 |
0.070 |
0.069 |
根据上表,估计在男性中,男性患色盲的概率为 .(结果精确到0.01)
如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A、B、C都在横格线上,若线段AB="4" cm,则线段BC= cm
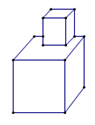
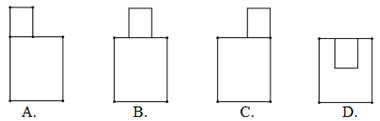
如图,已知矩形纸片的一条边经过直角三角形纸片的直角顶点,若矩形纸片的一组对边与直角三角形的两条直角边相交成∠1、∠2,则∠2-∠1= .
如图,已知Rt△ABC中,∠ABC=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF= .
如图,已知△ABC的三边长为 、
、 、
、 ,且
,且 ,若平行于三角形一边的直线
,若平行于三角形一边的直线 将△ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为
将△ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为 、
、 、
、 则
则 、
、 、
、 的大小关系是 (用“<”号连接).
的大小关系是 (用“<”号连接).
(本题满分8分)在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图。
(1)这50名同学捐款的众数为 元,中位数为 元
(2)求这50名同学捐款的平均数
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数
“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”。小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组
(1)小明被分配到“迷你马拉松”项目组的概率为
(2)求小明和小刚被分配到不同项目组的概率
如图,将□ABCD沿过点A的直线 折叠,使点D落到AB边上的点
折叠,使点D落到AB边上的点 处,折痕
处,折痕 交CD边于点E,连接BE
交CD边于点E,连接BE
(1)求证:四边形 是平行四边形
是平行四边形
(2)若BE平分∠ABC,求证:
扬州建城2500年之际,为了继续美化城市,计划在路旁栽树1200棵,由于志愿者的参加,实际每天栽树的棵树比原计划多20%,结果提前2天完成,求原计划每天栽树多少棵?
如图,已知⊙ 的直径AB=12cm,AC是⊙
的直径AB=12cm,AC是⊙ 的弦,过点C作⊙
的弦,过点C作⊙ 的切线交BA的延长线于点P,连接BC
的切线交BA的延长线于点P,连接BC
(1)求证:∠PCA=∠B
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长
平面直角坐标系中,点 的横坐标
的横坐标 的绝对值表示为
的绝对值表示为 ,纵[坐标
,纵[坐标 的绝对值表示为
的绝对值表示为 ,我们把点
,我们把点 的横坐标与纵坐标的绝对值之和叫做点
的横坐标与纵坐标的绝对值之和叫做点 的勾股值,记为:「
的勾股值,记为:「 」,即「
」,即「 」=
」= +
+ ,(其中的“+”是四则运算中的加法)
,(其中的“+”是四则运算中的加法)
(1)求点 ,
, 的勾股值「
的勾股值「 」、「
」、「 」
」
(2)点 在反比例函数
在反比例函数 的图像上,且「
的图像上,且「 」=4,求点
」=4,求点 的坐标;
的坐标;
(3)求满足条件「 」=3的所有点
」=3的所有点 围成的图形的面积
围成的图形的面积
科研所计划建一幢宿舍楼,因为科研所实验中会产生辐射,所以需要有两项配套工程:①在科研所到宿舍楼之间修一条笔直的道路;②对宿舍楼进行防辐射处理,已知防辐射费 万元与科研所到宿舍楼的距离
万元与科研所到宿舍楼的距离
 之间的关系式为:
之间的关系式为: (0≤
(0≤ ≤9),当科研所到宿舍楼的距离为1
≤9),当科研所到宿舍楼的距离为1 时,防辐射费用为720万元;当科研所到宿舍楼的距离为9
时,防辐射费用为720万元;当科研所到宿舍楼的距离为9 或大于9
或大于9 时,辐射影响忽略不计,不进行防辐射处理,设每公里修路的费用为
时,辐射影响忽略不计,不进行防辐射处理,设每公里修路的费用为 万元,配套工程费
万元,配套工程费 =防辐射费+修路费
=防辐射费+修路费
(1)当科研所到宿舍楼的距离为 =9
=9 时,防辐射费
时,防辐射费 = 万元;
= 万元; ,
,
(2)若每公里修路的费用为90万元,求当科研所到宿舍楼的距离为多少 时,配套工程费最少?
时,配套工程费最少?
(3)如果配套工程费不超过675万元,且科研所到宿舍楼的距离小于9 ,求每公里修路费用
,求每公里修路费用 万元的最大值
万元的最大值
如图,直线 ⊥线段
⊥线段 于点
于点 ,点
,点 在
在 上,且
上,且 ,点
,点 是直线
是直线 上的动点,作点
上的动点,作点 关于直线
关于直线 的对称点
的对称点 ,直线
,直线 与直线
与直线 相交于点
相交于点 ,连接
,连接
(1)如图1,若点 与点
与点 重合,则∠
重合,则∠ = °,线段
= °,线段 与
与 的比值为 ;
的比值为 ;
(2)如图2,若点 与点
与点 不重合,设过
不重合,设过 、
、 、
、 三点的圆与直线
三点的圆与直线 相交于
相交于 ,连接
,连接 。求证:①
。求证:① =
= ;②
;② =2
=2 ;
;
(3)如图3, ,
, ,则满足条件
,则满足条件 的点都在一个确定的圆上,在以下两小题中选做一题:
的点都在一个确定的圆上,在以下两小题中选做一题:
①如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB
②如果你不能发现这个确定圆的圆心和半径,那么请取几个特殊位置的 点,如点
点,如点 在直线
在直线 上、点
上、点 与点
与点 重合等进行探究,求这个圆的半径
重合等进行探究,求这个圆的半径
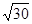
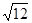

 = .
= . ,则
,则 .
.
 ,它的侧面展开图是一个半圆,则这个圆锥的高为 cm(结果保留根号)
,它的侧面展开图是一个半圆,则这个圆锥的高为 cm(结果保留根号)

 ,并把它的解集在数轴上表示出来
,并把它的解集在数轴上表示出来 粤公网安备 44130202000953号
粤公网安备 44130202000953号