初中数学相似多边形的性质选择题

如图，在矩形AOBC中，点A的坐标是(－2，1)，点C的纵坐标是4，则B，C两点的坐标分别是(  )

A．(，3)，(，4)	B．(，3)，(，4)
C．，(，4)	D．，(，4)

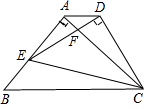
如图，在△ABC中，AD是高，△ABC的外接圆直径AE交BC边于点G，有下列四个结论：①AD²=BD•CD；②BE²=EG•AE；③AE•AD=AB•AC；④AG•EG=BG•CG．其中正确结论的个数是（　　）

A．1个

B．2个

C．3个

D．4个

如图，△ABC为等腰直角三角形，∠BAC=90°，BC=2，E为AB上任意一动点，以CE为斜边作等腰Rt△CDE，连接AD，下列说法：
①∠BCE=∠ACD；②AC⊥ED；③△AED∽△ECB；④AD∥BC；⑤四边形ABCD的面积有最大值，且最大值为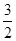．其中，正确的结论是            。

A．①②④

B．①③⑤

C．②③④

D．①④⑤

下列条件不能判定△ABC与△DEF相似的是（     ）

A．

B．，

C．∠A=∠D，∠B=∠E

D．，∠B=∠E

如图，在□ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF︰FC等于(  )

A．3︰2

B．3︰1

C．1︰1

D．1︰2

如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E，那么点D的坐标为

A．（，）

B．（，）

C．（，）

D．（，）

如图，阳光从教室的窗户射入室内，窗户框AB在地面上的影长DE＝1．8 m，窗户下沿到地面的距离BC＝1 m，EC＝1．2 m，那么窗户的高AB为  （  ）                        

A．2．16m

B．1．86m

C．1．6m

D．1．5m

如图，点P是菱形ABCD的对角线AC上的一个动点，过点P垂直于AC的直线交菱形ABCD的边于M、N两点．设AC＝2，BD＝1，AP＝x，△CMN的面积为y，则y关于x的函数图象大致形状是（ ）

在△ABC和△A₁B₁C₁中，有下列四个命题：
(1)若AB＝A₁B₁，AC＝A₁C₁，∠A＝∠A₁，则△ABC≌△A₁B₁C₁；
(2)若AB＝A₁B₁，AC＝A₁C₁，∠B＝∠B₁，则△ABC≌△A₁B₁C₁；
(3)若∠A＝∠A₁，∠C＝∠C₁，则△ABC∽△A₁B₁C₁；
(4)若AC︰A₁C₁＝CB︰C₁B₁，∠C＝∠C₁，则△ABC∽△A₁B₁C₁．
其中真命题的个数为(  )

A．4

B．3

C．2

D．1

如图，在△ABC中，AE交BC于点D，∠C＝∠E，AD︰DE＝3︰5，AE＝8，BD＝4，则DC的长等于(  )

A．

B．

C．

D．

如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，连结CN．若△CDN的面积与△CMN的面积比为1︰5，则 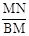的值为（    ）.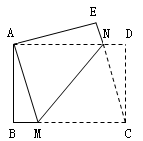

A．2

B．4

C．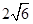

D．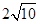

如图所示，在△ABC中，DE∥BC，DE分别与AB，AC相交于点D，E．若AD＝4，DB＝2，则DE︰BC的值为(  )

A．

B．

C．

D．

若 $\mathit{\Delta ABC}\backsim \mathit{\Delta DEF}$ ，相似比为 $3:2$ ，则对应高的比为 $($ 　　 $)$

A．

$3:2$

B．

$3:5$

C．

$9:4$

D．

$4:9$

如图，已知直线a∥b∥c，直线m、n与直线a、b、c分别交于点A、C、E、B、D、F，AC=4，CE=6，BD=3，则BF等于 （  ）                                            

A．7     B．8    C．7．5    D．8．5

若△ABC∽△DEF，AB＝5，BC＝3，DF＝7，EF＝9，则△ABC与△DEF的相似比是(  )

A．

B．

C．

D．