如图,P是Rt△ABC斜边AB上任意一点(A、B两点除外),过点P作一直线,使截得的三角形与Rt△ABC相似,这样的直线可以作( )

A、1条 B、2条 C、3条 D、4条
如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若 ,
, ,
,
则 的值为( )
的值为( )

A. |
B. |
C. |
D. |
如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是( )

A. |
B. |
C. |
D. |
将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=6,BC=8,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )

A. |
B. |
C. 或4 或4 |
D. 或4 或4 |
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )
后得到线段CD,则端点C的坐标为( )

| A.(3,3) | B.(4,3) | C.(3,1) | D.(4,1) |
如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )

A.1条 B.2条 C.3条 D.4条
一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是( )
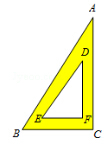
| A.5cm | B.6cm | C.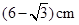 |
D. |
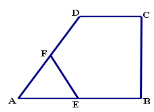
如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,CD=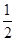 AB,点E、F分别为AB、AD的中点,则△AEF与多边形BCDFE的面积之比为 ( )
AB,点E、F分别为AB、AD的中点,则△AEF与多边形BCDFE的面积之比为 ( )
A、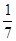 B、
B、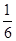 C、
C、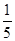 D、
D、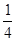
在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20 cm,则它的宽约为 ( )
| A.12.36 cm | B.13.6 cm | C.32.36 cm | D.7.64 cm |
如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③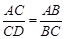 ; ④AC2=AD·AB.其中能够单独判定△ABC∽△ACD的条件个数为 ( )
; ④AC2=AD·AB.其中能够单独判定△ABC∽△ACD的条件个数为 ( )
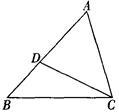
A.1 B.2 C.3 D.4
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )

A. |
B. |
C.2 | D.1 |