初中数学平行线分线段成比例试题

函数与在同一坐标系内的图像可以是(    )

如图，点A是反比例函数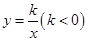 图像上的一点，过点A作AB⊥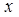轴于点B，且△AOB的面积为2，点A的坐标为．

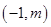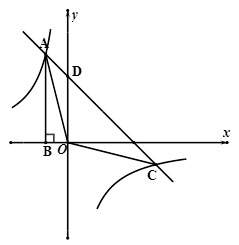
（1）求m和k的值． 
（2）若一次函数y=ax+3的图像经过点A，交双曲线的另一支于点C，交y轴于点D，求△AOC的面积．
（3）在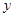轴上是否存在点P，使得△PAC的面积为6？如果存在，请求出点P的坐标；若不存在，请说明理由．

如图，已知A(-4，2)、B(n，-4)是一次函数y=kx+b的图象与反比例函数y= 的图象的两个交点．
　
（1）求此反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．

如图，A、B分别是反比例函数图象上的点，过A、B作轴的垂线，垂足分别为C、D，连接OB、OA，OA交BD于E点，△BOE的面积为，四边形ACDE的面积为，则  ．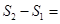

如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标（4，2），过点D（0，3）和E（6，0）的直线分别于AB，BC交于点M，N．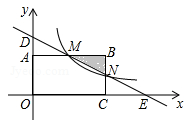

（1）求直线DE的解析式和点M的坐标；
（2）若反比例函数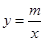（x＞0）的图象经过点M，求该反比函数的解析式，并通过计算判断点N是否在该函数的图象上．

如图，矩形OABC的顶点A，C的坐标分别是（4，0）（0，2），反比例函数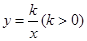的图像过对角线的交点P并且与AB，BC分别交于D，E两点，连接OD，OE，DE，则⊿ODE的面积为_____________．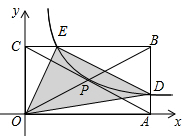

如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A，C分别在坐标轴上，点B的坐标为（4，2），直线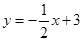交AB，BC于点M，N，反比例函数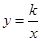的图象经过点M，N．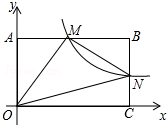

（1）求反比例函数的解析式；
（2）若点P在x轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．

已知双曲线y=与直线y=相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线y=上的动点．过点B作BD∥y轴交x轴于点D．过N（0，﹣n）作NC∥x轴交双曲线y=于点E，交BD于点C．

（1）若点D坐标是（﹣8，0），求A、B两点坐标及k的值；
（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式；
（3）设直线AM、BM分别与y轴相交于P、Q两点，且MA=pMP，MB=qMQ，求p﹣q的值．

九年级数学兴趣小组组织了以“等积变形”为主题的课题研究．
第一学习小组发现：如图（1），点A、点B在直线l₁上，点C、点D在直线l₂上，若l₁∥l₂，则S_△ABC=S_△ABD；反之亦成立．
第二学习小组发现：如图（2），点P是反比例函数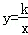上任意一点，过点P作x轴、y轴的垂线，垂足为M、N，则矩形OMPN的面积为定值|k|．

请利用上述结论解决下列问题：
（1）如图（3），四边形ABCD、与四边形CEFG都是正方形点E在CD上，正方形ABCD边长为2，则S_△BDF=　2　．
（2）如图（4），点P、Q在反比例函数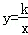图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若S_△PQG=8，则S_△POH=　2　，k=　﹣4　．
（3）如图（5）点P、Q是第一象限的点，且在反比例函数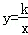图象上，过点P作x轴垂线，过点Q作y轴垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．

如图，平行四边形ABCD的顶点A、C在双曲线y₁=﹣上，B、D在双曲线y₂=上，k₁=2k₂（k₁＞0），AB∥y轴，S_▱ABCD=24，则k₁=　　．

如图，已知动点A在函数的图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA至点D，使AD=AB，延长BA至点E，使AE=AC．直线DE分别交x轴于点P，Q．当QE：DP=4：9时，图中阴影部分的面积等于　　．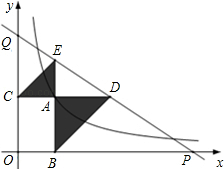

正方形的A₁B₁P₁P₂顶点P₁、P₂在反比例函数y= （x＞0）的图象上，顶点A₁、B₁分别在x轴、y轴的正半轴上，再在其右侧作正方形P₂P₃A₂B₂，顶点P₃在反比例函数y= （x＞0）的图象上，顶点A₂在x轴的正半轴上，则点P₃的坐标为　　．

如图，直线l₁：x=1，l₂：x=2，l₃：x=3，l₄：x=4，…，与函数y=（x＞0）的图象分别交于点A₁、A₂、A₃、A₄、…；与函数y=的图象分别交于点B₁、B₂、B₃、B₄、…．如果四边形A₁A₂B₂B₁的面积记为S₁，四边形A₂A₃B₃B₂的面积记为S₂，四边形A₃A₄B₄B₃的面积记为S₃，…，以此类推．则S₁₀的值是（　　）

A．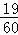

B．

C．

D．

如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数（k≠0）在第一象限内的图象经过点D、E，且D点的横坐标是它的纵坐标的2倍．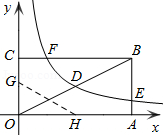

（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．

（本题满分分）某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系：

X（元）	3	4	5	6
y（个）	20	15	12	10

 
（1）根据表中的数据在平面直角坐标系中描出实数对（x,y）的对应点．
（2）猜测并确定y与x之间的函数关系式，并画出图象；
（3）设经营此贺卡的销售利润为w元，试求出w与x之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过10元／个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？