初中数学中心对称图形试题

我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等?
（1）阅读与说理：
对于这两个三角形均为直角三角形，显然它们全等．
对于这两个三角形均为钝角三角形，可证它们全等（证明略）.
对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
已知：如图所示，△ABC、△A₁B₁C₁均为锐角三角形，AB=A₁B₁，BC=B₁C_l，∠C=∠C_l.试说明△ABC≌△A₁B₁C₁的理由.
（请你将下列说理过程补充完整）.
理由：分别过点B，B₁作BD⊥CA于D，B₁ D₁⊥C₁ A₁于D₁.则∠BDC=∠B₁D₁C₁=90°，
因为BC=B₁C₁，∠C=∠C₁，△BCD≌△B₁C₁D₁，BD=B₁D₁.

（2）归纳与叙述：由（1）可得到一个正确结论，请你写出这个结论.

在中，，，直线经过点，且于，于.

（1）当直线绕点旋转到图1的位置时，求证：
①≌；
②；
（2）当直线绕点旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.

如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．
（1）求证：∠APB=∠BPH；
（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；
（3）设AP为x，四边形EFGP的面积为S，求出S与x的函数关系式，试问S是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

下列四种说法：
①若一个三角形三个内角的度数比为2∶3∶4，则这个三角形是锐角三角形；
②“掷两枚质地均匀的正方体骰子点数之和一定大于6”是必然事件；
③购买一张彩票可能中奖；
④已知等腰三角形的一个内角为40°，则这个等腰三角形的顶角为100°其中正确的序号是．

一个多边形的内角和与它的一个外角和为570°，则这个多边形的边数为（     ）

A．5

B．6

C．7

D．8

下列正多边形的组合中，能够铺满地面的是（     ）

A．正六边形和正方形	B．正五边形和正八边形
C．正六边形和正三角形	D．正十边形和正三角形

（11·佛山）如图物体从点A出发，按照A→B（第1步）→C（第2）→D→A
→E→F→G→A→B→……的顺序循环运动，则第2011步到达点     
   处；

（11·佛山）下列说法正确的是（          ）

A．“作线段CD＝AB”是一个命题；

B．三角形的三条内角平分线的交点为三角形的内心；

C．命题“若x＝1，则x^2＝1”的逆命题是真命题；

D．“具有相同字母的项称为同类项”是“同类项”的定义；

如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20^o，那么∠2的度数是（ ▲ )

A．30^o	B．25^o
C．20^o	D．15^o

如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，CE=4，求四边形ACEB的周长．

如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直．如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（　　）

A．	$600m$	B．	$500m$
C．	$400m$	D．	$300m$

如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）

A．30°	B．25°
C．20°	D．15°

将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如
图所示）．若∠C＝90°，BC＝8cm，则折痕DE的长度是   cm．

 

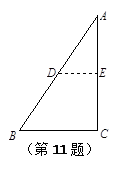如图，已知∠1=∠2，请你添加一个条件：______   _____，使△ABD≌△ACD。

已知一个几何体的三种视图如右图所示，则这个几何体是

A．圆柱

B．圆锥

C．球体

D．正方体