在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作 ,如图所示.若AB=4,AC=2,S1﹣S2=
,如图所示.若AB=4,AC=2,S1﹣S2= ,则S3﹣S4的值是( )
,则S3﹣S4的值是( )

A. |
B. |
C. |
D. |
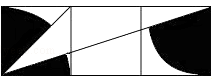
(年青海省中考)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 (结果保留π).
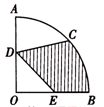
(年贵州省遵义市)如图,在圆心角为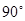 的扇形OAB中,半径OA=2
的扇形OAB中,半径OA=2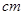 ,C为弧AB的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为
,C为弧AB的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为 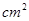 .
.
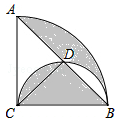
(年青海省西宁市)如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
A.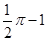 |
B.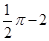 |
C.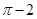 |
D.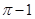 |
(年新疆、生产建设兵团)如图,在矩形ABCD中,CD=1,∠DBC=30°.若将BD绕点B旋转后,点D落在DC延长线上的点E处,点D经过的路径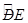 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )

A.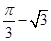 |
B. |
C.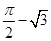 |
D.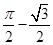 |
(年云南省)若扇形面积为3π,圆心角为60°,则该扇形的半径为( )
| A.3 | B.9 | C. |
D. |
(年贵州省贵阳市)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=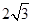 .
.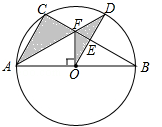
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
(年贵州省黔南州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=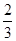 .
.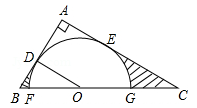
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
(本小题满分10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D
以AB上一点O为圆心作⊙O,使⊙O经过点A和点D。
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧 所围成的阴影部分的面积(结果保留根号和
所围成的阴影部分的面积(结果保留根号和 )。
)。
(本题满分10分)
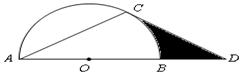
如图,点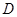 在
在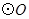 的直径
的直径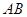 的延长线上,点
的延长线上,点 在
在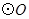 上,
上,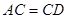 ,
,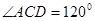 ,
,
(1)求证:
 是
是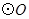 的切线;
的切线;(2)若
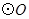 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.