如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是 .

如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为 cm.

如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是矩形,你所添加的条件是 (写出一种情况即可).

如图,已知 的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则
的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则 的周长为 cm.
的周长为 cm.

如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
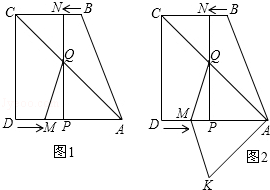
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
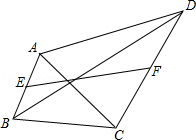
在四边形ABCD中,对角线AC⊥BD且AC=6、BD=8,E、F分别是边AB、CD的中点,则EF= .
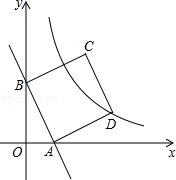
如图,矩形OBCD的顶点C的坐标为(1,3),则线段BD的长等于 .

如图,▱ABCD的对角线相交于点O,BC=7cm,BD=10cm,AC=6cm,则△AOD的周长为 cm.
已知菱形的两条对角线长分别是6和8,则这个菱形的面积为 .
如图,直线y=﹣2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y= 在第一象限经过点D.则k= .
在第一象限经过点D.则k= .
如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是 .

如图,在▱ABCD中,AB= ,AD=4,将▱ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .
,AD=4,将▱ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .

如图,▱ABCD的对角线AC与BD相交于点O,E为CD边中点,已知BC=6cm,则OE的长为 cm.

如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是 .

在▱ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE= .
