初中数学圆内接四边形的性质填空题

改写命题“对角线互相平分的四边形是平行四边形”：如果           ，那么        ．

如图，ABCD为正方形，A，E，F，G在同一条直线上，并且AE=5厘米，EF=3厘米，那么FG=        厘米．

一个多边形的每个外角都等于60°，这个多边形的内角和为             ．

正六边形的外角和是          ．

如图，将边长为8的正方形纸片ABCD折叠，使点B落在CD边的中点E上，压平后得到折痕MN，EF与AD边交于点G．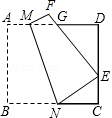

（1）求CN的长；
（2）求DG的长；
（3）AM=           ．（直接填结果）

如图，小明从A点出发，沿直线前进12米后向左转36°，再沿直线前进12米，又向左转36°…照这样走下去，他第一次回到出发地A点时，一共走了         米．

如图，在菱形ABCD中，点A在x轴上，点B的坐标为（8，2），点D的坐标为（0，2），则点C的坐标为             ．

如图，AB是⊙O的直径，OB=3，BC是⊙O的弦，∠ABC的平分线交⊙O于点D，连接OD，若∠BAC=20°，则的长等于         ．

如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：

①BE=CD；
②∠DGF=135°；
③∠ABG+∠ADG=180°；
④若，则．
其中正确的结论是        ．（填写所有正确结论的序号）

如图，在边长为的菱形ABCD中，∠A=60°，点E，F分别在AB，AD上，沿EF折叠菱形，使点A落在BC边上的点G处，且EG⊥BD于点M，则EG的长为    ．

如图，点E是▱ABCD的边AD的中点，连接CE交BD于点F，如果S_△DEF=a，那么S_△BCF=       ．

已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．

（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；
（提示：延长MF，交边BC的延长线于点H．）
（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；
（3）在（1），（2）的条件下，若BE=，∠AFM=15°，则AM=     ．

如图，平行四边形ABCD的对角线AC、BD相交于点O，BC=9，AC=8，BD=14，则△AOD的周长为       ．

如图，在平面直角坐标系中，点A和点B分别在x轴和y轴的正半轴上，OA=OB=a，以线段AB为边在第一象限作正方形ABCD，CD的延长线交x轴于点E，再以CE为边作第二个正方形ECGF，…，依此方法作下去，则第n个正方形的边长是         ．

如图，在Rt△ABC中，∠ACB=90°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF=BC．若AB=10，则EF的长是          ．