如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
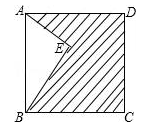
| A.48 | B.60 | C.76 | D.80 |
从多边形一个顶点出发的对角线把多边形分得2003个三角形,则这个多边形的边数为( ).
| A.2001 | B.2005 | C.2004 | D.2006 |
如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )

| A.48 | B.6 | C.76 | D.80 |
如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为

正n边形的每个内角都是120°,则n的值是( )
| A.3 | B.4 | C.6 | D.8 |
一个多边形的内角和是900°,则这个多边形的边数为( )
| A.6 | B.7 | C.8 | D.9 |
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
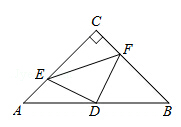
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个
如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )


如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
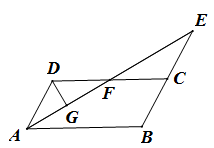
A. |
B.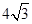 |
C.4 | D.8 |
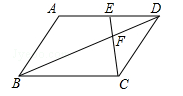
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则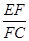 等于( )
等于( )
A.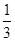 |
B.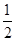 |
C.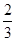 |
D.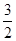 |