初中数学圆试题

如图，在□ABCD中，E、F分别在AD、BC边上，且AE=CF．请你猜想BE与DF的关系，并说明理由．

如果一个正多边形的内角和是1440°，则这个正多边形是正边形。

将矩形纸片ABCD按如图方式折叠，BE、CF为折痕，折叠后点B和点D都落在点O处．若△EOF是等边三角形，则的值为                ．

图①是一面矩形彩旗完全展平时的尺寸图（单位：cm）．其中矩形ABCD是由双层白布缝制的穿旗杆用的旗裤，阴影部分DCEF为矩形绸缎旗面．
（1）用经加工的圆木杆穿入旗裤作旗杆，求旗杆的最大直径（精确到1cm）；
（2）将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为220cm．在无风的天气里，彩旗自然下垂，如图②．求彩旗下垂时最低处离地面的最小高度h．

如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（      ）

A．48

B．6

C．76

D．80

若一个多边形外角和与内角和相等，则这个多边形是          边形．

一个多边形的内角和是900°，则这个多边形的边数为（ ）

A．6

B．7

C．8

D．9

如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．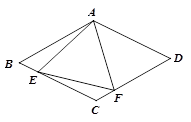

（1）证明不论E、F在BC．CD上如何滑动，总有BE=CF；
（2）当点E、F在BC．CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．

已知菱形的周长为，一条对角线长为，则这个菱形的面积为           （）．

如图，半径为2的两圆⊙O₁和⊙O₂均与轴相切于点，反比例函数（）的图像与两圆分别交于点A、B、C、D，则图中阴影部分的面积是       ．

如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于（ ）

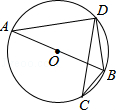
A．116°

B．32°

C．58°

D．64°

如图，△ABC内接于⊙O，∠B=60º，∠A=40º，半径OE⊥AB，连接CE，则∠E=（  ）

A．5º

B．10º

C．15º

D．20º

如图，在△ABC中，∠ABC＝90°，D是边AC上的一点，连接BD，使∠A＝2∠1，E是BC上的一点，以BE为直径的圆O经过点D

（1）求证：AC是⊙O的切线；
（2）若∠A＝60°，⊙O的半径为2，求阴影部分的面积（结果保留根号和π）．

如图，圆锥体的高，底面半径，则圆锥体的侧面积为________．

如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠AOD等于（  ）

A．120°

B．140°

C．150°

D．160°