初中数学圆试题

在平行四边形ABCD中，∠A：∠B：∠C=2：3：2，则∠D=（ ）

A．36°

B．108°

C．72°

D．60°

如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，若∠A=100°，则∠1+∠2+∠3+∠4=    ．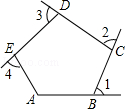

如图，在△ABC中，AB=5，BC=6，AC=7，点D，E，F分别是△ABC三边的中点，则△DEF的周长为（ ）

A．9

B．10

C．11

D．12

一个平行四边形的两条对角线的长分别为8和10，则这个平行四边形边长不可能是（ ）

A．2

B．5

C．8

D．10

已知菱形ABCD的两条对角线分别长6和8，则它的面积是              ．

在▱ABCD中，若∠A+∠C=160°，则∠C的度数为          ．

如图，在正方形ABCD中，AB=2cm，对角线AC、BD交于点O，点E以一定的速度从A向B移动，点F以相同的速度从B向C移动，连结OE、OF、EF．

（1）△AOE≌△        ；
（2）线段EF的最小值是         cm．

如图，四边形ABCD的对角线交于点O，从下列条件：①AD∥BC，②AB=CD，③AO=CO，④∠ABC=∠ADC中选出两个可使四边形ABCD是平行四边形，则你选的两个条件是      ．（填写一组序号即可）

如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（ ）

A、△ABD与△ABC的周长相等
B、△ABD与△ABC的面积相等
C、菱形的周长等于两条对角线之和的两倍
D、菱形的面积等于两条对角线之积的两倍

如图，矩形ABCD中，点E，F分别在AB，CD边上，连接CE、AF，∠DCE=∠BAF．试判断四边形AECF的形状并加以证明．

如图，平行四边形ABCD中，∠ABC=60°，E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，EF=，则AB的长是（  ）

A．0．5

B．1

C．1．5

D．2

下列命题中是真命题的有（  ）个．
①相等的角是对顶角；
②两直线被第三条直线所截，内错角相等；
③若m²=n²，则m=n；
④平行四边形的对角线互相平分；
⑤一组对边平行，一组对边相等的四边形是平行四边形．

A．0

B．1

C．2

D．3

一个多边形的每个内角均为108°，则这个多边形是（  ）边形．

A．4

B．5

C．6

D．7

一个凸多边形的内角和是其外角和的2倍，则这个多边形是         边形．

如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为（ ）

A．4

B．7

C．3

D．12