(年云南省昆明市)如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.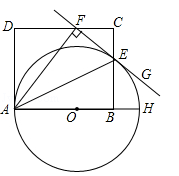
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
(年青海省中考)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.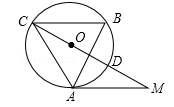
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
(年新疆乌鲁木齐市)如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=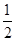 ,AB=3,求BD的长.
,AB=3,求BD的长.
(年贵州省遵义市)如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.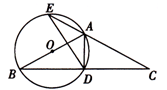
(1)求证:D是BC的中点;
(2)若DE=3,BD—AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
(年贵州省贵阳市)如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
(年贵州省毕节)如图,将▱ABCD的AD边延长至点E,使DE= AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.
(年贵州省贵阳市)“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是 .

(年贵州省黔东南州)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )

A. |
B. |
C.12 | D.24 |
(年贵州省铜仁市)如图,在矩形ABCD中,BC=6,CD=3,将△BCD沿对角线BD翻折,点C落在点C1处,BC1交AD于点E,则线段DE的长为( )

| A.3 | B. |
C.5 | D. |
(年云南省曲靖市)如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
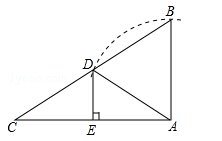
(年江西省南昌市)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .
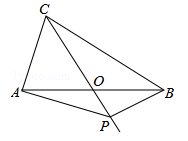
(年青海省西宁市)如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为 .
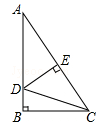
(黔西南州)如图所示,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切
(2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4.求弦CE的长.
我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A,B重合),D是半圆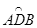 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.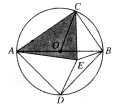
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.