初中数学平行线的性质试题

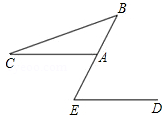
（年云南省曲靖市）如图，过∠AOB平分线上一点C作CD∥OB交OA于点D，E是线段OC的中点，请过点E画直线分别交射线CD、OB于点M、N，探究线段OD、ON、DM之间的数量关系，并证明你的结论．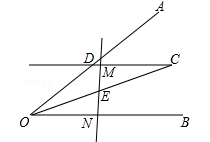

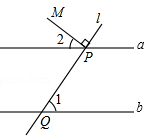
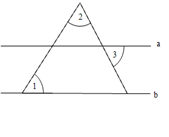
（年青海省中考）如图，直线a∥b，直线l与a相交于点P，与直线b相交于点Q，且PM垂直于l，若∠1=58°，则∠2=          ．

（年云南省）如图，直线l₁∥l₂，并且被直线l₃，l₄所截，则∠α=          ．

（年蒙自市初中学业水平第一次模拟测试）如图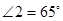，，，，则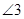的大小为        ．

（年新疆、生产建设兵团）已知，AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（ ）

A．53°

B．63°

C．73°

D．83°

（年新疆乌鲁木齐市）如图，直线a∥b，∠1=108°，则∠2的度数是（ ）

A．72°

B．82°

C．92°

D．108°

（年贵州省毕节）如图，直线a∥b，直角三角形ABC的顶点B在直线a上，∠C=90°，∠β=55°，则∠α的度数为（ ）

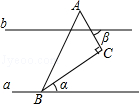
A．15°

B．25°

C．35°

D．55°

（年贵州省遵义市）如图，直线∥，若∠1=，则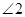的度数为（   ）．

A．

B．

C．

D．

（年云南省昆明市）如图，在△ABC中，∠B=40°，过点C作CD∥AB，∠ACD=65°，则∠ACB的度数为（ ）

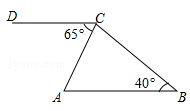
A．60°

B．65°

C．70°

D．75°

如图，AD∥BC，∠D=100°，CA平分∠BCD，则∠DAC=          度．

如图，直线a∥b，AC⊥BC，∠C=90°，则∠α=            °．

如图，OP∥QR∥ST，若∠2=110°，∠3=120°，则∠1=__________．

问题探究：

1．新知学习

若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”，其“面线”被该平面图形截得的线段叫做该平面图形的“面径”（例如圆的直径就是圆的“面径”）．

2．解决问题

已知等边三角形ABC的边长为2．

（1）如图一，若 $\mathit{AD}\perp \mathit{BC}$，垂足为D，试说明AD是△ABC的一条面径，并求AD的长；

（2）如图二，若 $\mathit{ME}\parallel \mathit{BC}$，且ME是△ABC的一条面径，求面径ME的长；

（3）如图三，已知D为BC的中点，连接AD，M为AB上的一点 $（0＜\mathit{AM}＜1）$，E是DC上的一点，连接ME，ME与AD交于点O，且 $S_{△\mathit{MOA}}＝S_{△\mathit{DOE}}$．

①求证：ME是△ABC的面径；

②连接AE，求证： $\mathit{MD}\parallel \mathit{AE}$；

（4）请你猜测等边三角形ABC的面径长l的取值范围（直接写出结果）