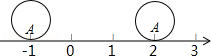如图, 蒙古包可近似地看作由圆锥和圆柱组成, 若用毛毡搭建一个底面圆面积为 ,圆柱高为 ,圆锥高为 的蒙古包, 则需要毛毡的面积是

A . B . C . D .
如图,在 中, , , ,把 绕 所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为
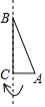
A. B. C. D.
“赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图.已知底面圆的直径 ,圆柱体部分的高 ,圆锥体部分的高 ,则这个陀螺的表面积是

A. B. C. D.
由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为
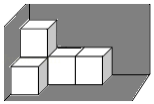
A.9B.11C.14D.18
空间任意选定一点 ,以点 为端点,作三条互相垂直的射线 、 、 .这三条互相垂直的射线分别称作 轴、 轴、 轴,统称为坐标轴,它们的方向分别为 (水平向前)、 (水平向右)、 (竖直向上)方向,这样的坐标系称为空间直角坐标系.
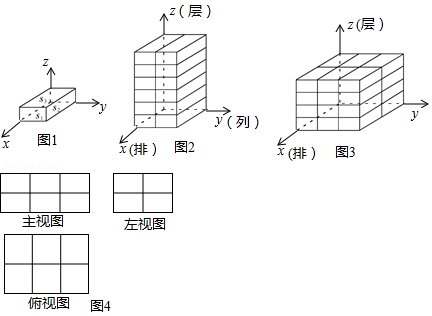
将相邻三个面的面积记为 、 、 ,且 的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体 所在的面与 轴垂直, 所在的面与 轴垂直, 所在的面与 轴垂直,如图1所示.
若将 轴方向表示的量称为几何体码放的排数, 轴方向表示的量称为几何体码放的列数, 轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了1排2列6层,用有序数组记作 ,2, ,如图3的几何体码放了2排3列4层,用有序数组记作 ,3, .这样我们就可用每一个有序数组 , , 表示一种几何体的码放方式.
(1)如图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为 ,组成这个几何体的单位长方体的个数为 个;
(2)对有序数组性质的理解,下列说法正确的是 ;(只填序号)
①每一个有序数组 , , 表示一种几何体的码放方式.
②有序数组中 、 、 的乘积就表示几何体中单位长方体的个数.
③有序数组不同,所表示几何体的单位长方体个数不同.
④不同的有序数组所表示的几何体的体积不同.
⑤有序数组中 、 、 每两个乘积的2倍可分别确定几何体表面上 、 、 的个数.
(3)为了进一步探究有序数组 , , 的几何体的表面积公式 ,某同学针对若干个单位长方体进行码放,制作了下列表格:
| 几何体 有序数组 |
单位长方体的个数 |
表面上面积为 的个数 |
表面上面积为 的个数 |
表面上面积为 的个数 |
表面积 |
| ,1, |
1 |
2 |
2 |
2 |
|
| ,2, |
2 |
4 |
2 |
4 |
|
| ,1, |
3 |
2 |
6 |
6 |
|
| ,1, |
4 |
4 |
8 |
4 |
|
| ,5, |
5 |
10 |
2 |
10 |
|
| ,2, |
6 |
12 |
6 |
4 |
|
| ,1, |
7 |
14 |
14 |
2 |
|
| ,2, |
8 |
8 |
8 |
8 |
|
|
|
|
|
|
|
|
根据以上规律,请写出有序数组 , , 的几何体表面积计算公式 ;(用 、 、 、 、 、 表示)
(4)当 , , 时,对由12个单位长方体码放的几何体进行打包,为了节约外包装材料,对12个单位长方体码放的几何体表面积最小的规律进行探究,根据探究的结果请写出使几何体表面积最小的有序数组,并用几何体表面积公式求出这个最小面积.(缝隙不计)
某几何体的三视图及相关数据(单位: 如图所示,则该几何体的侧面积是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走 个小立方块.
如图是由7个完全相同的小立方块搭成的几何体,已知每个小立方块的棱长为2cm.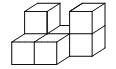
(1)画出该几何体的三视图;
(2)求出该几何体的表面积.
由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为

| A. |
18 |
B. |
15 |
C. |
12 |
D. |
6 |
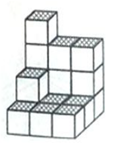
如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小正方体,王亮所搭几何体表面积为________________.
如图,有一个高为5的圆柱体,现在它的底面圆周在数轴上滚动,在滚动前圆柱体底面圆周上有一点A和数轴上表示-1的点重合,当圆柱体滚动一周时A点恰好落在了表示2的点的位置.则这个圆柱体的侧面积是 .