某学校要种植一块面积为 的长方形草坪,要求两边长均不小于 ,则草坪的一边长为 (单位: 随另一边长 (单位: 的变化而变化的图象可能是
A. B.
B.
C. D.
D.
已知正比例函数 和反比例函数 ,在同一直角坐标系下的图象如图所示,其中符合 的是

| A. |
①② |
B. |
①④ |
C. |
②③ |
D. |
③④ |
如图,菱形 的边长为2, ,一个以点 为顶点的 角绕点 旋转,这个角的两边分别与线段 的延长线及 的延长线交于点 、 ,设 , ,则能大致反映 与 的函数关系的图象是
A.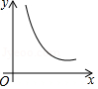 B.
B.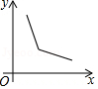
C.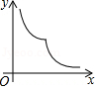 D.
D.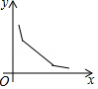
已知反比例函数 的图象分别位于第二、第四象限, , 、 , 两点在该图象上,下列命题:①过点 作 轴, 为垂足,连接 .若 的面积为3,则 ;②若 ,则 ;③若 ,则 ,其中真命题个数是
| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
二次函数 的图象如图所示,则一次函数 和反比例函数 在同一平面直角坐标系中的图象可能是

A.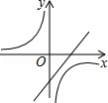 B.
B.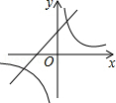
C. D.
D.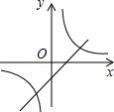
将 的图象向右平移1个单位长度,再向上平移1个单位长度所得图象如图,则所得图象的解析式为

| A. |
|
B. |
|
C. |
|
D. |
|
已知二次函数 的图象如下,则一次函数 与反比例函数 在同一平面直角坐标系中的图象大致是

A.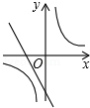 B.
B.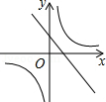
C.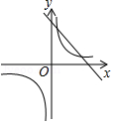 D.
D.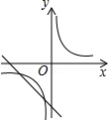
已知二次函数 的图象如图所示,则一次函数 的图象和反比例函数 的图象在同一坐标系中大致为
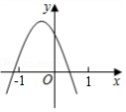
| A. |
|
B. |
|
| C. |
|
D. |
|
用数形结合等思想方法确定二次函数 的图象与反比例函数 的图象的交点的横坐标 所在的范围是
| A. |
|
B. |
|
C. |
|
D. |
|