初中数学两条直线相交或平行问题试题

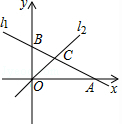
如图，在平面直角坐标系中，直线 l ₁： y＝﹣ $\frac{\sqrt{2}}{4}$ x+1与 x轴， y轴分别交于点 A和点 B，直线 l ₂： y＝ kx（ k≠0）与直线 l ₁在第一象限交于点 C．若∠ BOC＝∠ BCO，则 k的值为（　　）

A．

$\frac{\sqrt{2}}{3}$

B．

$\frac{\sqrt{2}}{2}$

C．

$\sqrt{2}$

D．

2 $\sqrt{2}$

已知直线l₁：y＝﹣3x+b与直线l₂：y＝﹣kx+m在同一坐标系中的图象交于点（1，﹣2），那么方程组 $\left\{\begin{array}{c}3x+y=b\\ \mathit{kx}+y=m\end{array}\right.$的解是（　　）

A． $\left\{\begin{array}{c}x=1\\ y=-2\end{array}\right.$B． $\left\{\begin{array}{c}x=1\\ y=2\end{array}\right.$C． $\left\{\begin{array}{c}x=-1\\ y=-2\end{array}\right.$D． $\left\{\begin{array}{c}x=-1\\ y=2\end{array}\right.$

如图，直线 $l_1:y=x+3$ 与过点 $A(3,0)$ 的直线 $l_2$ 交于点 $C(1,m)$ ，与 $x$ 轴交于点 $B$ ．

（1）求直线 $l_2$ 的解析式；

（2）点 $M$ 在直线 $l_1$ 上， $\mathit{MN}//y$ 轴，交直线 $l_2$ 于点 $N$ ，若 $\mathit{MN}=\mathit{AB}$ ，求点 $M$ 的坐标．

如图，直线、是常数与直线交于点，则关于的不等式的解集为　   　．

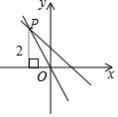
如图，正比例函数的图象与一次函数的图象相交于点，点到轴的距离是2，则这个正比例函数的解析式是　　．

已知点，到直线的距离可表示为，例如：点到直线的距离．据此进一步可得两条平行线和之间的距离为　　．

如图，在 $\text{Rt}\Delta \text{ABO}$ 中， $\angle \mathit{OBA}=90°$ ， $A(4,4)$ ，点 $C$ 在边 $\mathit{AB}$ 上，且 $\frac{\mathit{AC}}{\mathit{CB}}=\frac{1}{3}$ ，点 $D$ 为 $\mathit{OB}$ 的中点，点 $P$ 为边 $\mathit{OA}$ 上的动点，当点 $P$ 在 $\mathit{OA}$ 上移动时，使四边形 $\mathit{PDBC}$ 周长最小的点 $P$ 的坐标为 $($ 　　 $)$

A．

$(2,2)$

B．

$(\frac{5}{2}$ ， $\frac{5}{2})$

C．

$(\frac{8}{3}$ ， $\frac{8}{3})$

D．

$(3,3)$

如图，直线经过点，当时，的取值范围为　　．

如图，在平面直角坐标系中，直线 $l_1:y=\frac{\sqrt{3}}{3}x+1$ 与直线 $l_2:y=\sqrt{3}x$ 交于点 $A_1$ ，过 $A_1$ 作 $x$ 轴的垂线，垂足为 $B_1$ ，过 $B_1$ 作 $l_2$ 的平行线交 $l_1$ 于 $A_2$ ，过 $A_2$ 作 $x$ 轴的垂线，垂足为 $B_2$ ，过 $B_2$ 作 $l_2$ 的平行线交 $l_1$ 于 $A_3$ ，过 $A_3$ 作 $x$ 轴的垂线，垂足为 $B_3\dots$ 按此规律，则点 $A_n$ 的纵坐标为 $($ 　　 $)$

A．

${\left(\frac{3}{2}\right)}^n$

B．

${\left(\frac{1}{2}\right)}^n+1$

C．

${\left(\frac{3}{2}\right)}^{n-1}+\frac{1}{2}$

D．

$\frac{3^n-1}{2}$

如图，已知过点的直线与直线相交于点．

（1）求直线的解析式；

（2）求四边形的面积．

将直线向下平移个单位后，与直线的交点在第二象限，则的取值范围是　　．

元朝朱世杰的《算学启蒙》一书记载：“今有良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何日追及之．”如图是两匹马行走路程关于行走时间的函数图象，则两图象交点的坐标是　　．

在平面直角坐标系中（如图），已知一次函数的图象平行于直线，且经过点，与轴交于点．

（1）求这个一次函数的解析式；

（2）设点在轴上，当时，求点的坐标．

若直线 $l_1$ 经过点 $(0,4)$ ， $l_2$ 经过点 $(3,2)$ ，且 $l_1$ 与 $l_2$ 关于 $x$ 轴对称，则 $l_1$ 与 $l_2$ 的交点坐标为 $($ 　　 $)$

A．

$(-2,0)$

B．

$(2,0)$

C．

$(-6,0)$

D．

$(6,0)$

如图，已知直线 $l_1:y=-2x+4$ 与直线 $l_2:y=\mathit{kx}+b(k\ne 0)$ 在第一象限交于点 $M$ ．若直线 $l_2$ 与 $x$ 轴的交点为 $A(-2,0)$ ，则 $k$ 的取值范围是 $($ 　　 $)$

A．

$-2<k<2$

B．

$-2<k<0$

C．

$0<k<4$

D．

$0<k<2$