有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数 与 的图象性质.
小明根据学习函数的经验,对函数 与 ,当 时的图象性质进行了探究.
下面是小明的探究过程:
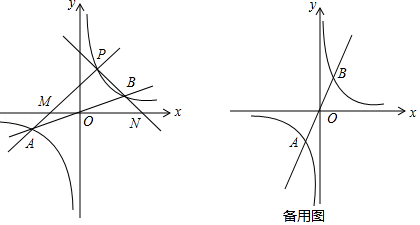
(1)如图所示,设函数 与 图象的交点为 , ,已知 点的坐标为 ,则 点的坐标为 ;
(2)若点 为第一象限内双曲线上不同于点 的任意一点.
①设直线 交 轴于点 ,直线 交 轴于点 .求证: .
证明过程如下:设 ,直线 的解析式为 .
则 ,
解得
直线 的解析式为
请你把上面的解答过程补充完整,并完成剩余的证明.
②当 点坐标为 , 时,判断 的形状,并用 表示出 的面积.