某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有 张桌子时,两种摆放方式各能坐多少人?
张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?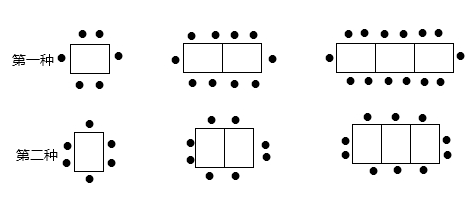
有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步.已知小明的速度为4米/秒,小狗的速度为12米/秒.跑步的时间记为 秒.在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为
秒.在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为 米.
米.
(1)当 秒和
秒和 秒时,分别求
秒时,分别求 的值?
的值?
(2)当 时,请用含
时,请用含 的代数式表示
的代数式表示 .
.
(3)当 时,请用含
时,请用含 的代数式表示
的代数式表示 .(可直接写出结果)
.(可直接写出结果)
下图方式摆放餐桌和椅子:

(1)1张餐桌可坐4人,2张餐桌可坐 人。
(2)按照上图的方式继续排列餐桌,完成下表。
| 桌子张数 |
3 |
4 |
n |
| 可坐人数 |
|
|
|
将连续的正整数1,2,3,4,…,排列成如下的数表,用3×3的方框框出9个数(如图).
(1)图中方框框出的9个数的和与方框正中间的数10有什么关系?
(2)将方框上下左右平移,但一定要框住数表中的9个数.若设正中间的数为a,用含a的代数式表示方框框住的9个数字,并计算这9个数的和.
(3)能否在方框中框出9个数,使这9个数的和为270?若能,求出这9个数;若不能,请说明理由.
初步探索 感悟方法
如图1,用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点,以格点为顶点的多边形叫格点多边形,设格点多边形的面积为S,它各边上格点的个数和为x.

(1)如图1中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式,答:S= .
| 多边形的序号 |
① |
② |
③ |
④ |
… |
| 多边形的面积S |
2 |
|
3 |
|
… |
| 各边上格点的个数和x |
4 |
5 |
6 |
|
… |
(2)你可以画些格点多边形,使这些多边形内部都有而且只有2个格点.
此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S= .
(3)请你继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x、n之间的关系式S= .(用含有字母x、n的代数式表示)
积累经验 拓展延伸
如图2,对等边三角形网格中的类似问题进行探究:等边三角形网格中每个小等边三角形的面积为1,小等边三角形的顶点为格点,以格点为顶点的多边形称为格点多边形.
(4)设格点多边形的面积为S,它各边上格点的个数和为x,当格点多边形内部有且只有n个格点时,猜想S与x、n之间的关系式S= .(用含有字母x、n的代数式表示)