如图，每个图案都由若干个棋子摆成，依照此规律，第n个图案中棋子的总个数可以用含n的代数式表示为 ．
某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元．“国庆节”
期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的90%付款．
现某客户要到该商场购买西装20套，领带x条（x＞20）．
（1）若该客户按方案一购买，需付款 元．（用含x的代数式表示）
若该客户按方案二购买，需付款 元．（用含x的代数式表示）
（2）若x=30，通过计算说明此时按（1）哪种方案购买较为合算？
（3）当x=30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．
如图，长方形的长为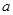
，宽为
，
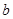（1）用含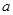、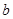的代数式表示右图阴影部分的面积S阴影．
（2）当a=5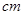
，b=2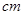时，求S阴影．（
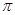取3．14）
一个矩形的周长为30，若矩形的一边长用字母
表示，则此矩形的面积为（ ）
A． |
B． |
C． |
D． |
如图，平面内有公共端点的6条射线O
| A．O | B．O | C．O | D．OE、OF，按照图中的规律，从射线OA开始，按照逆时针方向，依次在射线上画点表示1，2，3，4，5，6，7，… |
（1）根据图中规律，表示“19”的点在射线 上；
（2）按照图中规律推算，表示“2014”的点在射线 上；
（3）请你写出在射线OC上表示的数的规律（用含
的代数式表示） ．
全班同学排成长方形长队，每排的同学数为a，排数比每排同学数的3倍还多2，那么全班同学数是（ ）
A． |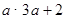
B． |
C． |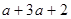
D． |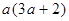
某餐厅中，一张桌子可坐6人，有以下两种摆放方式：
（1）当有
张桌子时，两种摆放方式各能坐多少人？
（2）一天中午餐厅要接待98位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？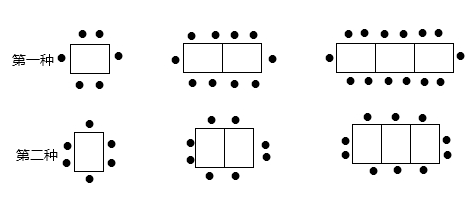
下表中的图形是由火柴棒搭接而成，请推测第n个图形有________根火柴棍．
某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90%付款．
现某客户要到该服装厂购买西装20套，领带x条（x＞20）．
（1）若该客户按方案①购买，需付款 元（用含x的代数式表示）；
若该客户按方案②购买，需付款 元（用含x的代数式表示）；
（2）若x=30，通过计算说明此时按哪种方案购买较为合算？
扬州万家福商场将进货价80元的某品牌童装，以120元的销售价售出，平均每天能售出20件．则单件利润为120－80=40元，每天的盈利为40×20=800元．为了迎接“六一”儿童节，商场决定采取适当的降价措施．经调査，如果每件童装降价1元，那么平均每天就可多售出2件．（盈利=单件利润×销售量）
（1）若每件童装的销售价下降2元，则：
①降价后，每件童装的销售价为______________元；
②降价后，每件童装的利润为______________元；
③降价后，商场平均每天的销售量为__________________件．
（2）若设每件童装的销售价下降a元，试用含a的代数式填空：
①降价后，每件童装的销售价为______________元；
②降价后，每件童装的利润为______________元；
③降价后，商场平均每天的销售量为__________________件．
（3）如果商场要想平均每天销售这种童装盈利1200元．商场经理甲说“在原售价每件120元的基础上再下降20元，可以完成任务”，商场经理乙说“不用降那么多，在原售价每件120元的基础上再下降10元就可以了”，试判断经理甲与乙的说法是否正确，并说明理由．
操作与思考：
操作：将长为1，宽为
的长方形纸片（
），如图那样折一下，剪下一个边长等于长方形宽度的正方形（称为第一次操作）；再把剩下的长方形如图那样折一下，剪下一个边长等于此时长方形宽度的正方形（称为第二次操作）．如此反复操作下去，若在第n次操作后剩下的长方形是正方形，则操作终止．
思考：
（1）第一次操作后，剩下的长方形的边长分别为 、 ．（用含的式子表示）
（2）如果第二次操作后剩下的长方形恰好是正方形，则的值是 ．
（3）第三次操作后，若剩下的长方形恰好是正方形，试求的值．
粤公网安备 44130202000953号
的2倍与
的
的和”用代数式表示为 ．
