在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
(1)实验操作:在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中:
(2)观察发现:任一次平移,点P可能到达的点在我们学过的一种函数的图象上,如:平移1次后在函数 的图象上;平移2次后在函数 的图象上……由此我们知道,平移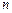 次后在函数 的图象上.(请填写相应的解析式)
次后在函数 的图象上.(请填写相应的解析式)
(3)探索运用:点P从点O出发经过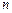 次平移后,到达直线
次平移后,到达直线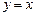 上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
上的点Q,且平移的路径长不小于50,不超过56,求点Q的坐标.
如图,根据要求回答下列问题:
(1)点A关于y轴对称点A'的坐标是____________;
点B关于y轴对称点B'的坐标是______________;
点C关于y轴对称点C'的坐标是______________;
(2)作出与△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
某医药研究所开发了一种新药,在试验药效时发现,假如成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时的变化如图所示,当成人按规定剂量服药后,
(1)分别求出 x≤2和 x≥2时,y 与x之间的函数关系式
(2)假如每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.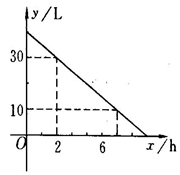
(1)求y与x的函数解析式.
(2)一箱油可供拖位机工作几小时?
已知一次函数y=kx+b的图像经过点(-2,-4),且与正比例函数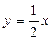 的图像相交于点(4,a)。
的图像相交于点(4,a)。
求:
(1)a的值;
(2)k、b的值;
(3)画出这两个函数图像,并求出它们与y轴所围成的三角形的面积.
已知一次函数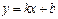 的图像经过点(-1,-5),且与正比例函数
的图像经过点(-1,-5),且与正比例函数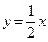 的图像相交于点(2,
的图像相交于点(2,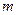 ).
).
(1)求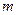 的值;
的值;
(2)求一次函数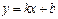 的解析式;
的解析式;
(3)这两个函数图像与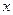 轴所围成的三角形面积.
轴所围成的三角形面积.