读故事想问题。
在数学上也不乏“此时无声胜有声”的小故事。1903年,在纽约的一次数学报告会上,数学家科勒上了讲台,他没说一句话,知识用粉笔在黑板上写了两个算式,一个是67个2相乘减1,另一个是193707721×761838257287,并演算出结果。两个算式的结果完全相同,这时,全场爆发出经久不息的掌声。这是为什么呢?
因为科勒解决了200年来一直没有弄清的一个问题,即67个2相乘减1的结果是不是质数?现在既然它等于另外另个数的乘积,因此证明67个2相乘再减1不是质数,而是合数。
科勒只作了一个简短的无声的报告,可这是他花了3年中全部星期天的试卷才得出的结论。在这简单算式中所蕴涵的智慧、毅力和努力,比洋洋洒洒的万言报告更具魅力。
请你用数学概念说明为什么67个2相乘再减1的结果不是质数而是合数。
一条公路上,有一个骑车人和一个步行人,骑车人速度是步行驶速度的3倍,每隔6分钟有一辆公共汽车超过步行人,每隔10分钟有一辆公共汽车超过骑车人,如果公共汽车始发站发车时间隔不变,那么多少分钟发一辆公共汽车?
有一种新型电子闹钟,每到正点和半点都响一次铃,每过9分亮一次灯。如果12点时,它既响了铃,又亮了灯,那么下一次既响铃又亮灯是什么时间?
有一对互相咬合的齿轮,大齿轮有28个齿,小齿轮有20个齿。大小两个齿轮的某两个齿从第一相遇到第二次相遇(转动的齿轮总数相同),大小两个齿轮各转了 多少圈?
在下面的括号里填上适当的质数,使这个式子成立。此题共有( )种填法(交换加数位置,算同一种填法)。( )+( )=30。
| A.2 | B.3 | C.4 | D.5 |
2008年8月24日,第29届奥运会在北京圆满落下帷幕.为了奥运各项赛事的顺利进行,在北京、上海、青岛新建或改建了一系列奥运场馆: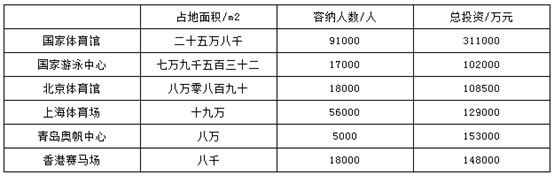
⑴用数字表示各体育馆的占地面积。
⑵把总投资数四舍五入到亿元。
已知M=4322×1233,N=4321×1234,下面结论正确的是( )
| A.M>N | B.M=N | C.M<N | D.无法判断 |
有5瓶维生素,其中一瓶少了4片.如果用天平称,至少称 次就能找到少药片的那瓶.
一个六位数由三个“8”和三个“0”组成,如果从这个数读出两个“零”,那么这个六位数是 .