字母A、B、C、D、E、F和数字1、9、9、3分别按以下变动次序发生变化：
A、B、C、D、E、F、1、9、9、3 （原来）
B、C、D、E、F、A、9、9、3、1 （第一次变动）
C、D、E、F、A、B、9、3、1、9 （第二次变动）
D、E、F、A、B、C、3、1、9、9 （第三次变动）
…
问：至少经过多少次变动后，字母和数字将变回原来的顺序？
下面是一张月历卡。
| 日 |
一 |
二 |
三 |
四 |
五 |
六 |
| |
|
|
|
1 |
2 |
3 |
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 18 |
19 |
20 |
21 |
22 |
23 |
24 |
| 25 |
26 |
27 |
28 |
29 |
30 |
31 |
用形如
的框，每次框出4个数，一共可以框出多少个不同的和？
下面是一张4×4的方格纸，它是由16个同样大小的正方形组成的，而且每个正方形里都写了一个数。从这张方格纸上去掉一个 
,一共有多少种不同的去法？
| 1 |
2 |
3 |
4 |
| 5 |
6 |
7 |
8 |
| 9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
16 |
下表中，一张半透明的正方形纸盖住了9个数，在表中移动这张纸，可以使每次盖住的9个数的和各不相同。一共可以盖住多少个不同的和？
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
| 31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
| 41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
在下表中，每次圈出相邻的两个数，一共可以得到多少个不同的和？
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
在下边算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。当爱=" ______" 、好=" ______" 、学=" ______" 、习=" ______" 时，算式成立。
| |
1 |
6 |
学 |
| + |
|
好 |
好 |
| = |
爱 |
学 |
习 |
如图所示，把自然数中的偶数2，4，6，8，…，依次排成5列，如果各列从左到右依次称为第1列、第2列、第3列、第4列和第5列，那么，数1986出现在第几列?
1999名学生从前往后排成一列，按下面的规则报数：如果某个同学报的数是一位数，后面的同学就要报出这个数与9的和；如果某个同学报的数是两位数，后面的同学就要报出这个数的个位数与6的和．现在让第一个同学报l，那么最后一个同学报的数是多少?
在l，9，8，9后面顺次写出一串数字，使得每个数字部等于它前面两个数字之和的个位数字，即得到
l，9，8，9，7，6，3，9，2，l，3，4，…．
那么这个数串的前398个数字的和是多少?
请在图所示的8个小圆圈内，分别填入1，2，3，4，5，6，7，8这8个数字，使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好分别是l，2，3，4，5，6，7。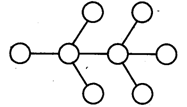
将1、2、3、5、6、7、9、10、11填人图中的小圆圈内，使得每条直线上各数之和都相等．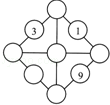
请将1至9这9个数填入图中的方框内，使得所有不等号都成立．所有满足要求的填法共有多少种？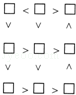
如图，在3×3的方格表的每个方格中填入恰当的数，使得每行、每列、每条对角线上所填数之和都相等．
粤公网安备 44130202000953号