高中物理计算题

如图所示，一透明介质制成的直角三棱镜，顶角∠A＝30°，一束光由真空垂直射向AC面，经AB面射出后的光线偏离原来方向15°。已知光在真空中的传播速度为c。求：
①该介质对光的折射率；
②光在介质中的传播速度。

某压力锅结构如图所示。盖好密封锅盖，将压力阀套在出气孔上，给压力锅加热。
①在压力阀被顶起前，停止加热。若此时锅内气体的体积为V、摩尔体积为V₀，阿伏加德罗常数为N_A，计算锅内气体的分子数。
②在压力阀被顶起后，停止加热。假设放气过程中气体对外界做功为W₀，并向外界释放了Q₀的热量。求该过程锅内原有气体内能的变化量。

质谱仪是一种分析同位素的重要工具，它的构造原理如图所示。离子源S产生质量为m、电荷量为q的钾离子，离子出来时速度很小，可视为零。离子经过电势差为U的电场加速后，沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场，经半圆周到达照相底片上的P点。

(1)求粒子进入磁场时的速度；
(2)求P点到入口S₁的距离x；
(3)在实验过程中由于仪器不完善，加速电压在平均值U附近变化U，求需要以多大相对精确度U/U维持加速电压值，才能使钾39、钾41的同位素束在照相底片上不发生覆盖。

在水平地面上放置一长木板A，木板中心O处有一小物块B(视为质点)，开始时A、B均静止，长木板运动的速度随时间变化的关系图像如图所示，A与B之间的动摩擦因数为0.1，m_B=2kg，取g=10m/s²。回答以下问题：

(1)若B不从A上滑下，在图乙中画出B的速度随时间变化的关系图线。
(2)若B不从A上滑下，板的最短长度L；
(3)从B开始运动直到最终静止时A与B之间因摩擦而产生的热量。

如图所示，两根足够长、相距为L的金属直角导轨，它们各有一边在同一水平面内，另一边垂直于水平面。一绝缘细线跨过导轨直角顶点处定滑轮连接两金属细杆ab、cd，杆通过两端金属小圆环垂直套在导轨上，细杆质量均为m、电阻均为R，整个装置处于磁感强度大小为B，方向竖直向上的匀强磁场中。保持细线拉直后同时无初速释放两细杆，cd杆下降高度h时达到最大速度。 ab杆一直在水平导轨上运动，接触处摩擦及导轨电阻均不计，取重力加速度为g。求：

(1)刚释放时，ab杆的加速度大小；
(2)下滑过程中，cd杆的最大速率；
(3)从开始释放到刚好达到最大速度的过程中整个回路所产生的热量。

某个光子是氢原子核外电子从n=4跃迁到n=1时所发出的，已知普朗克常量h=6.63×10^-34J·s，求：
①该光子的能量为多少eV？频率为多少Hz?
②该光子的动量大小为多少？

如图所示为一直角棱镜ABC，光从空气中以入射角θ从AB面上的P点进入棱镜，在AC面恰无光线射出。
①求棱镜的折射率。
②要使该光线能从AC面射出，θ角应如何变化？

在做“用油膜法测分子的大小”实验时，油酸酒精溶液的浓度为每10⁴ml溶液中有纯油酸5mL，用注射器测得1mL上述溶液有液滴75滴。把1滴该溶液滴入盛水的浅盘里，待水面稳定后，将玻璃板放在浅盘上，在玻璃板上描出油酸膜的轮廓，随后把玻璃板放在坐标纸上，计算得到轮廓范围内小正方形的个数为100个，已知坐标中小正方形的边长为1cm，求：
①该次实验中1滴油酸酒精溶液中纯油酸的体积是多少m³?      
②按以上数据，估测出油酸分子的直径是多少?

如图所示空间分为Ⅰ，Ⅱ，Ⅲ三个足够长的区域，各边界面相互平行，其中Ⅰ，Ⅱ区域存在匀强电场E_I＝1.0×10⁴ V/m，方向垂直边界面竖直向上；E_Ⅱ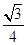＝×10⁵ V/m，方向水平向右，Ⅲ区域磁感应强度B＝5.0 T，方向垂直纸面向里，三个区域宽度分别为d₁＝5.0 m，d₂＝4.0 m，d₃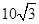＝ m．一质量m＝1.0×10^－8 kg、电荷量q＝1.6×10^－6C的粒子从O点由静止释放，粒子重力忽略不计．求：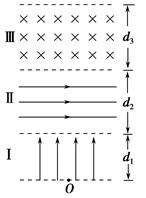

(1)粒子离开区域Ⅰ时的速度大小；
(2)粒子从区域Ⅱ进入区域Ⅲ时的速度方向与边界面的夹角；
(3)粒子从O点开始到离开Ⅲ区域时所用的时间．

如图甲所示，一正方形金属线框位于有界匀强磁场区域内，线框的右边紧贴着边界．t＝0时刻对线框施加一水平向右的外力F，让线框从静止开始做匀加速直线运动，经过时间t₀穿出磁场．图乙所示为外力F随时间t变化的图象．若线框质量为m、电阻R及图象中的F₀、t₀均为已知量，则根据上述条件，请你推出：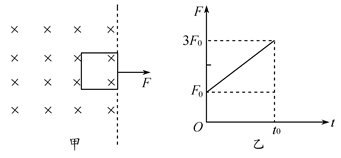

(1)磁感应强度B的表达式；
(2)线框左边刚离开磁场前瞬间的感应电动势E的表达式．

如图所示的电路中，两平行金属板A、B水平放置，两板间的距离d="40" cm。电源电动势E=24V,内电阻r="1" Ω，电阻R="15" Ω。闭合开关S，待电路稳定后，将一带正电的小球从B板小孔以初速度v₀="4" m/s竖直向上射入板间。若小球带电量为q=1×10^-2 C,质量为m=2×10^-2 kg,不考虑空气阻力。那么，

(1)滑动变阻器接入电路的阻值为多大时，小球恰能到达A板.
(2)此时，电源的输出功率是多大.(取g="10" m/s²)

某同学欲测直角三棱镜ABC的折射率n．他让光线沿平行于BC边的方向射到三棱镜的侧面AB上，经棱镜AB边和AC边的两次折射和BC边的一次反射后，又从另一侧面AC边上的P点射出．

①在右面图上画出光路图；
②若将射向AB边的光的入射角调整为α＝60°，此时的折射角γ＝30°，求折射率n的值．

如图所示，一导热性能良好、内壁光滑的气缸开口向上竖直放置，横截面积为S＝2×l0^-3m²、质量与厚度均不计的活塞，与气缸底部之间封闭了一部分气体，此时活塞与气缸底部之间的距离为24cm.大气压强P₀＝l.0×10⁵Pa.现将质量为4kg的物块放在活塞上，取g＝10m/s².求：

①稳定后活塞与气缸底部之间的距离；
②分析说明上述过程气体是吸热还是放热.

如图所示，在平面直角坐标系xOy平面内存在着方向相反的两个匀强磁场区域，其中圆心在坐标原点、半径为R的圆形区域Ⅰ内磁场方向垂直于xOy平面向里，第一象限和第四象限的圆形区域外（区域Ⅱ）的磁场方向垂直于xOy平面向外，MN为与x轴垂直且与y轴相距2.5R的一条直线，现有一质量为m、电荷量为+q的带电粒子，经过加速电压为U的加速电场加速后，从坐标为(－R，0)的A点沿x轴正方向射入区域Ⅰ，并从横坐标为0.5R处的P点进入区域Ⅱ．已知粒子第一次经过直线MN和第二次经过直线MN时的速度方向恰好相反，不计粒子重力，求：

（1）粒子进入圆形区域Ⅰ时的运动速度v的大小；       
（2）区域Ⅰ和Ⅱ中磁感应强度B₁、B₂的大小；
（3）粒子从A点开始到第二次经过直线MN的过程中运动的总时间t.

如图所示，圆心角为90°的光滑圆弧形轨道，半径为1.6m，其底端切线沿水平方向．长为的斜面，倾角为60°，其顶端与弧形轨道末端相接，斜面正中间有一竖直放置的直杆，现让质量为1Kg的物块从弧形轨道的顶端由静止开始滑下，物块离开弧形轨道后刚好能从直杆的顶端通过，重力加速度取10m/s²，求：

（1）物块滑到弧形轨道底端时对轨道的压力大小；
（2）直杆的长度为多大．