高中物理计算题

一辆汽车从A点由静止出发做匀加速直线运动，用t=" 4" s的时间通过一座长x=" 24" m的平桥BC，过桥后的速度是v_c=" 9" m/ s.求：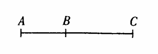

(1)它刚开上桥头时的速度v_B有多大？
(2)桥头与出发点相距多远？

如图所示，在xoy竖直平面内，长L的绝缘轻绳一端固定在第一象限的P点,另一端栓有一质量为m、带电荷量为+q的小球,OP距离也为L且与x轴的夹角为60∘.在x轴上方有水平向左的匀强电场,场强大小为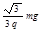,在x轴下方有竖直向上的匀强电场,场强大小为mg/q,过O和P两点的虚线右侧存在方向垂直xOy平面向外、磁感应强度为B的匀强磁场。小球置于y轴上的C点时,绳恰好伸直且与y轴夹角为30∘，小球由静止释放后将沿CD方向做直线运动，到达D点时绳恰好绷紧，小球沿绳方向的分速度立即变为零，并以垂直于绳方向的分速度摆下，到达O点时将绳断开。不计空气阻力。求：

(1)小球刚释放瞬间的加速度大小a；
(2)小球到达O点时的速度大小v；
(3)小球从O点开始到最终离开x轴的时间t.

光滑水平面上有一质量为M的滑块，滑块的左侧是一光滑的圆弧，圆弧半径为R=1m．一质量为m的小球以速度v₀向右运动冲上滑块．已知M=4m，g取10m/s²，若小球刚好没跃出圆弧的上端，求：

（1）小球的初速度v₀是多少？
（2）滑块获得的最大速度是多少？

如图所示，在光滑的水平桌面上有一长为L＝2 m的木板C，它的两端各有一块挡板，C的质量为m_C＝5 kg，在C的中央并排放着两个可视为质点的滑块A与B，其质量分别为m_A＝1 kg、m_B＝4 kg，开始时A、B、C均处于静止状态，并且A、B间夹有少许炸药，炸药爆炸使得A以v_A＝6 m/s的速度水平向左运动，不计一切摩擦，两滑块中任意一块与挡板碰撞后就与挡板合成一体，爆炸与碰撞时间不计，求：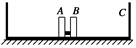

(1)当两滑块都与挡板碰撞后，板C的速度多大？
(2)从爆炸开始到两个滑块都与挡板碰撞为止，板C的位移多大？方向如何？

如图所示，在光滑的水平面上有一质量为m，长度为l的小车，小车左端有一质量也是m可视为质点的物块。车子的右壁固定有一个处于锁定状态的压缩轻弹簧（弹簧长度与车长相比可忽略），物块与小车间动摩擦因数为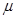，整个系统处于静止。现在给物块一个水平向右的初速度v₀，物块刚好能与小车右壁的弹簧接触，此时弹簧锁定瞬间解除，当物块再回到左端时，与小车相对静止。求：

（1）物块的初速度v₀；
（2）在上述整个过程中小车相对地面的位移。

(1)从宏观现象中总结出来的经典物理学规律不一定都能适用于微观体系。但是在某些问题中利用经典物理学规律也能得到与实际比较相符合的结论。
例如，玻尔建立的氢原子模型，仍然把电子的运动看做经典力学描述下的轨道运动。他认为，氢原子中的电子在库仑力的作用下，绕原子核做匀速圆周运动。已知电子质量为m，电荷为e，静电力常量为k，氢原子处于基态时电子的轨道半径为r₁。
(1)氢原予处于基态时，电子绕原子核运动，可等效为环形电流，求此等效电流值。
(2)在微观领域，动量守恒定律和能量守恒定律依然适用。
a．己知光在真空中的速度为c，氢原子在不同能级之间跃迁时，跃迁前后可认为质量不变，均为m。设氢原子处于基态时的能量为E₁(E₁<O)，当原子处于第一激发态时的能量为E₁/4，求原子从第一激发态跃迁到基态时，放出光子的能量和氢原子的反冲速度。
b．在轻核聚变的核反应中，两个氘核(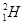)以相同的动能E_o=0.35MeV做对心碰撞，假设该反应中释放的核能全部转化为氦核(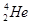)和中子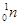（）的动能。已知氘核的质量m_D=2.0141u，中子的质量m_n=1.0087u，氦核的质量M_He=3.0160u，其中1u相当于931MeV。在上述轻核聚变的核反应中生成的氦核和中子的动能各是多少MeV（结果保留1位有效数字）?

如图所示水平传送带，轮的半径均为 1/π，顺时针转动，两轮轴心相距L=8.0m。将一物体轻放在传送带左端，物体与传送带间的动摩擦因数为μ=0.4。

（1）当传送带以v₀=4.0m/s的速度匀速运动时,物体由A端运送到B端所用时间为多少?
（2）要想尽快将物体由A端送到B端（设初速度仍为零），轮的转速至少应为多大?
（3）在运送物体的过程中物体会在传送带上留下划痕。当物体静止释放在A端时，传送带做初速度v₀ =    m/s的匀减速运动，物体刚好到达B端，求传送带的加速度大小和划痕的长度 。（结果可用分数表示）

如图所示，一个内壁光滑的圆柱形汽缸，高度为L、底面积为S，缸内有一个质量为m的活塞，封闭了一定质量的理想气体．温度为热力学温标T₀时，用绳子系住汽缸底，将汽缸倒过来悬挂起来，汽缸处于竖直状态，缸内气体高为L₀.已知重力加速度为g，大气压强为p₀，不计活塞厚度及活塞与缸体的摩擦，求：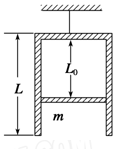

（1）采用缓慢升温的方法使活塞与汽缸脱离，缸内气体的温度至少要升高到多少？
（2）从开始升温到活塞刚要脱离汽缸，缸内气体压力对活塞做功多少
（3）当活塞刚要脱离汽缸时，缸内气体的内能增加量为ΔU，则气体在活塞下移的过程中吸收的热量为多少？

浙江卫视六频道《我老爸最棒》栏目中有一项人体飞镖项目，该运动简化模型如图所示。某次运动中，手握飞镖的小孩用不可伸长的细绳系于天花板下，在A处被其父亲沿垂直细绳方向推出，摆至最低处B时小孩松手，飞镖依靠惯性飞出击中竖直放置的圆形靶最低点D点，圆形靶的最高点C与B在同一高度，C、O、D在一条直径上，A、B、C三处在同一竖直平面内，且BC与圆形靶平面垂直。已知飞镖质量m=1kg，BC距离s=8m，靶的半径R=2m，AB高度差h=0.8m，g取10m/s²。不计空气阻力，小孩和飞镖均可视为质点。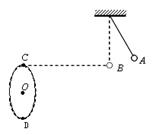

（1）求孩子在A处被推出时初速度v_o的大小；
（2）若小孩摆至最低处B点时沿BC方向用力推出飞镖，飞镖刚好能击中靶心，求在B处小孩对飞镖做的功W；
（3）在第(2)小题中，如果飞镖脱手时沿BC方向速度不变，但由于小孩手臂的水平抖动使其获得了一个垂直于BC的水平速度v，要让飞镖能够击中圆形靶，求v的取值范围。

(16分)如图所示，光滑的平行金属导轨水平放置，电阻不计，导轨间距为l，左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场，磁场宽度为s。一质量为m、电阻为r的金属棒MN置于导轨上，与导轨垂直且接触良好，受到F＝0.5v＋0.4(N)(v为金属棒速度)的水平外力作用，从磁场的左边界由静止开始运动，测得电阻两端电压随时间均匀增大.(已知：l＝1m，m＝1kg，R＝0.3Ω，r＝0.2Ω，s＝1m)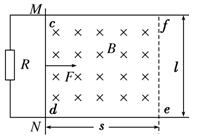

(1)判断该金属棒在磁场中是否做匀加速直线运动；
(2)求加速度的大小和磁感应强度B的大小；
(3)若撤去外力后棒的速度v随位移x的变化规律满足v＝v₀－x，且棒在运动到ef处时恰好静止，则外力F作用的时间为多少？
(4)若在棒未出磁场区域时撤出外力，画出棒在整个运动过程中速度随位移变化所对应的各种可能的图线.

磁悬浮列车的运动原理如图所示，在水平面上有两根很长的平行直导轨，导轨间有与导轨垂直且方向相反的匀强磁场B₁和B₂，B₁和B₂相互间隔，导轨上有金属框abcd。当磁场B₁和B₂同时以恒定速度沿导轨向右匀速运动时，金属框也会沿导轨向右运动。已知两导轨间距L₁="0." 4 m，两种磁场的宽度均为L₂，L₂=ab，B₁＝B₂=B=1.0T。金属框的质量m="0.1" kg，电阻R=2.0Ω。设金属框受到的阻力与其速度成正比，即f=kv，比例系数k="0." 08 kg/s。求：

（1）若金属框达到某一速度时，磁场停止运动，此后某时刻金属框的加速度大小为a=6.0m/s²，则此时金属框的速度v₁多大？
（2）若磁场的运动速度始终为v₀=5m/s，在线框加速的过程中，某时刻线框速度v′=2m/s，求此时线框的加速度a′的大小
（3）若磁场的运动速度始终为v₀=5m/s，求金属框的最大速度v₂为多大？此时装置消耗的功率为多大？

如图所示，两根足够长的金属导轨ab、cd与水平面成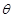=37固定，导轨间距离为L=1m，电阻不计。在导轨上端接一个阻值为R₀的定值电阻。在c、N之间接有电阻箱。整个系统置于匀强磁场中，磁感应强度方向与导轨所在平面垂直，磁感应强度大小为B="1" T；现将一质量为m、电阻可以忽略的金属棒MN从图示位置由静止开始释放。金属棒下滑过程中与导轨接触良好。金属棒与导轨间的滑动摩擦因数为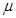="0." 5。改变电阻箱的阻值R，测定金属棒的最大速度v_m，得到v_m-R的关系如图所示。若轨道足够长，重力加速度g取10。求：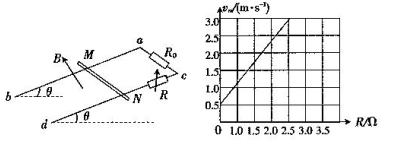

(1)金属杆的质量m和定值电阻 R₀的阻值；
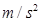(2)当电阻箱R取3.5 时，且金属杆的加速度为l 时，此时金属杆的速度。

一长为L的细绳固定在O点，O点离地高度大于L，另一端系一质量为m的小球，开始时细绳与水平方向的夹角为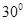，如图甲所示。求小球释放后，运动到最低点时对绳的拉力多大？

用如图甲所示的滑轮组提升水中的物体M₁，动滑轮A所受重力为G₁，物体M₁完全在水面下以速度v匀速竖直上升的过程中，卷扬机加在绳子自由端的拉力为F₁，拉力F₁做功的功率为P₁，滑轮组的机械效率为；为了提高滑轮组的机械效率，用所受重力为G₂的动滑轮B替换动滑轮A，如图乙所示，用替换动滑轮后的滑轮组提升水中的物体M₂，物体M₂完全在水面下以相同的速度v匀速竖直上升的过程中，卷扬机加在绳子自由端的拉力为F₂，拉力F₂做功的功率为P₂，滑轮组的机械效率为。已知：G₁－G₂=30N，－=5%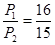，，M₁、M₂两物体的质量相等，体积V均为4×10^-2m³，g取10N/kg，绳重、轮与轴的摩擦及水的阻力均可忽略不计。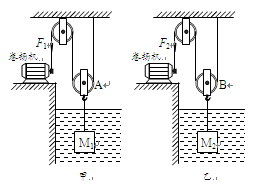

求：（1）物体M₁受到的浮力F_浮；
（2）拉力F₁与F₂之比；
（3）物体M₁受到的重力G。

如图是工人提升物体的装置示意图，其中AB是一个不计重力、可以绕O点转动的杠杆，且AO:OB=2:5，杠杆B端系有重为1056N物体D，杠杆A端固定着滑轮组。质量为60kg的工人站在水平地面上，他对地面的压强p₀=1.2×10⁴Pa。当他利用该装置匀速提升重物M时，物体D受到的支持力为N₁，工人对地面的压强p₁=0.8×10⁴Pa，此时滑轮组的机械效率η=90%；当工人利用该装置匀速提升重物N时，物体D受到的支持力为N₂，工人竖直向下的拉力为F₂；已知N₁: N₂="5:" 2，每个滑轮质量都相等，绳重及滑轮与轴的摩擦不计，g取10N/kg。求：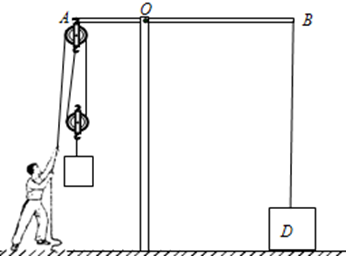

（1）提升重物M时工人竖直向下的拉力F₁。
（2）提升重物N以0.5m/s的速度匀速上升时工人拉力的功率P。