高中物理计算题

如图为“用DIS（位移传感器、数据采集器、计算机）研究加速度和力的关系”的实验装置。

（1）在该实验中必须采用控制变量法，应保持___________不变，用钩码所受的重力作为___________，用DIS测小车的加速度。
（2）改变所挂钩码的数量，多次重复测量。在某次实验中根据测得的多组数据可画出a-F关系图线（如图所示）。

①分析此图线的OA段可得出的实验结论是_________________________________。
②此图线的AB段明显偏离直线，造成此误差的主要原因是

A．小车与轨道之间存在摩擦	B．导轨保持了水平状态
C．所挂钩码的总质量太大	D．所用小车的质量太大

圆心为O、半径为r的圆形区域中有一个磁感应强度为B、方向垂直于纸面向里的匀强磁场，与区域边缘的最短距离为L的处有一竖直放置的荧屏MN，今有一质量为m的电子以速率v从左侧沿方向垂直射入磁场，越出磁场后打在荧光屏上之P点，如图所示，求的长度和电子通过磁场所用的时间。

有一电阻，其阻值大约在40～50Ω之间，需要进一步测定其阻值，手边现有下列器材：

器　　材 代号 规　　　　　格 电池组 电压表 电流表 电流表 滑动变阻器 滑动变阻器 电键 几根连接用的导线 E V A1 A2 R1 R2 S 电动势9V，内阻约0.5Ω 量程0V～10V，内阻20kΩ 量程0mA～50mA,内阻约20Ω 量程0mA～300mA,内阻约4Ω 阻值范围为0Ω～100Ω，额定电流1A 阻值范围为0Ω～1700Ω，额定电流0.3A

 

 
有两种可供选用的电路如图10-4-18所示，
实验要求多测几组电流、电压值，以便画
出电流－电压关系图．
为了实验能正常进行并减小测量误差，而且要
求滑动变阻器便于调节，在实验中应选图　　
所示的电路，应选代号是　　的电流表和代号
是　　的滑动变阻器．

（1）如图1所示，为一固定在竖直平面内的光滑轨道，段水平，段与段平滑连接。质量为的小球从高位处由静止开始沿轨道下滑，与静止在轨道段上质量为的小球发生碰撞，碰撞后两球两球的运动方向处于同一水平线上，且在碰撞过程中无机械能损失。求碰撞后小球的速度大小。

（2）碰撞过程中的能量传递规律在屋里学中有着广泛的应用。为了探究这一规律，我们才用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的恶简化力学模型。如图2所示，在固定光滑水平轨道上，质量分别为的若干个球沿直线静止相间排列，给第1个球初能，从而引起各球的依次碰撞。定义其中第个球经过依次碰撞后获得的动能与之比为第1个球对第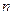个球的动能传递系数。
a.求；

b.若为确定的已知量。求为何值时，值最大。

在场强为的水平匀强磁场中，一质量为、带正电的小球在静止释放，小球的运动曲线如图所示．已知此曲线在最低点的曲率半径为该点到轴距离的2倍，重力加速度为．求：
(1)小球运动到任意位置的速率

(2)小球在运动过程中第一次下降的最大距离.

(3)当在上述磁场中加一竖直向上场强为的匀强电场时，小球从静止释放后获得的最大速率．

1932年，劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示，置于高真空中的D形金属盒半径为，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计。磁感应强度为的匀强磁场与盒面垂直。处粒子源产生的粒子，质量为、电荷量为 ，在加速器中被加速，加速电压为。加速过程中不考虑相对论效应和重力作用。

（1） 求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比；

（2） 求粒子从静止开始加速到出口处所需的时间 ；

（3） 实际使用中，磁感应强度和加速电场频率都有最大值的限制。若某一加速器磁感应强度和加速电场频率的最大值分别为、，试讨论粒子能获得的最大动能。

"探究加速度与物体质量、物体受力的关系"的实验装置如图甲所示.
（1）在平衡小车与桌面之间摩擦力的过程中，打出了一条纸袋如图乙所示。计时器打点的时间间隔为0.02.从比较清晰的点起，每5个点取一个计数点，量出相邻计数点之间的距离。该小车的加速度=.（结果保留两位有效数字）

（2）平衡摩擦力后，将5个相同的砝码都放在小车上.挂上砝码盘，然后每次从小车上取一个砝码添加到砝码盘中，测量小车的加速度。小车的加速度与砝码盘中砝码总重力F的实验数据如下表

砝码盘中砝码总重力()	0.196	0.392	0.588	0.784	0.980
加速度（）	0.69	1.18	1.66	2.18	2.70

请根据实验数据作出的关系图像

（3）根据提供的试验数据作出的图线不通过原点，请说明主要原因。

一气象探测气球，在充有压强为（即）、温度为的氦气时，体积为。在上升至海拔高空的过程中，气球内氦气逐渐减小到此高度上的大气压，气球内部因启动一持续加热过程而维持其温度不变。此后停止加热，保持高度不变。已知在这一海拔高度气温为。求：
（1）氦气在停止加热前的体积；

（2）氦气在停止加热较长一段时间后的体积。

如图，是边长为的正方形。质量为、电荷量为的电子以大小为的初速度沿纸面垂直于边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从边上的任意点入射，都只能从点射出磁场。不计重力，求：

（1）次匀强磁场区域中磁感应强度的方向和大小；

（2）此匀强磁场区域的最小面积。

利用图（a）实验可粗略测量人吹气产生的压强。两端开口的细玻璃管水平放置，管内塞有潮湿小棉球，实验者从玻璃管的一端吹气，棉球从另一端飞出，测得玻璃管内部截面积，距地面高度，棉球质量，开始时的静止位置与管口的距离，落地点与管口的水平距离。然后多次改变，测出对应的，画出关系图线，如图（b）所示，并由此得出相应的斜率。

（1）若不计棉球在空中运动时的空气阻力，根据以上测得的物理量可得，棉球从端飞出的速度＝。
（2）假设实验者吹气能保持玻璃管内气体压强始终为恒定值，不计棉球与管壁的摩擦，重力加速度，大气压强均为已知，利用图（b）中拟合直线的斜率可得，管内气体压强＝。
（3）考虑到实验时棉球与管壁间有摩擦，则（2）中得到的与实际压强相比（填偏大、偏小）。

①在“长度的测量”实验中，调整游标卡尺两侧脚间距离，主尺和游标的位置如图所示，此时卡尺两脚间狭缝宽度为_______mm；若要狭缝宽度调到0.20mm，应使游标上除0刻度线外第_______条刻度线与主尺上表示_________mm的刻度线对齐。
     
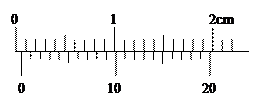
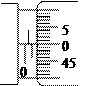
②如图所示，螺旋测微器测出的金属丝的直径是__________mm．

质量m=2.0×10^-4kg、电荷量q=1.0×10^-6C的带正电微粒静止在空间范围足够大的匀强电场中，电场强度大小为E₁．在t=0时刻，电场强度突然增加到E₂=4.0×10³N/C，场强方向保持不变．到t=0.20s时刻再把电场方向改为水平向右，场强大小保持不变．取g=10m/s²．求：
（1）原来电场强度E₁的大小？
（2）t=0.20s时刻带电微粒的速度大小？
（3）带电微粒运动速度水平向右时刻的动能？

汤姆生用如29所示的装置（阴极射线管）发现了电子。电子由阴极C射出，在CA间电场加速，A'上有一小孔，所以只有一细束的电子可以通过P与P'两平行板间的区域，电子通过这两极板区域后打到管的末端，使末端S处的荧光屏发光（荧光屏可以近似看成平面。）。水平放置的平行板相距为d，长度为L，它的右端与荧光屏的距离为D。当平行板间不加电场和磁场时，电子水平打到荧光屏的O点；当两平行板间电压为U时，在荧光屏上S点出现一亮点，测出OS=H；当偏转板中又加一磁感应强度为B垂直纸面向里的匀强磁场时，发现电子又打到荧光屏的O点。若不考虑电子的重力，求
（1）CA间的加速电压U'；
（2）电子的比荷e/m。

右下图为一真空示波管的示意图，电子从灯丝K发出（初速度可忽略不计），经灯丝与A板间的电压U₁加速，从A板中心孔沿中心线KO射出，然后进入两块平行金属板M、N形成的偏转电场中（偏转电场可视为匀强电场），电子进入M、N间电场时的速度与电场方向垂直，电子经过电场后打在荧光屏上的P点。已知M、N两板间的电压为U₂，两板间的距离为d，板长为L，电子的质量为m，电荷量为e，不计电子受到的重力及它们之间的相互作用力。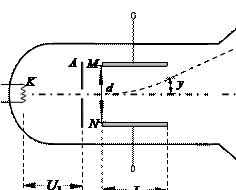

（1）求电子穿过A板时速度的大小；
（2）求电子从偏转电场射出时的侧移量；
（3）若要使电子打在荧光屏上P点的上方，可采取哪些措施？

如图所示，在平行金属板AB间和BC间分别由电源提供恒定的电压U₁和U₂，且U₂＞U₁。在A板附近有一电子，质量为m,电荷量为-e,由静止开始向右运动，穿过B板的小孔进人BC之间，若AB间距为d₁，BC间距为d₂。求：
（1）电子通过B板小孔后向右运动距B板的最大距离；
（2）电子在AC间往返运动的周期。