如图所示,设A、B为地球赤道圆的一条直径的两端,利用地球同步卫星将一电磁波信号由A传播到B,至少需要几颗同步卫星?这几颗同步卫星间的最近距离是多少?用这几颗同步卫星把电磁波信号由A传播到B需要的时间是多少?(已知地球半径R,地表面处的重力加速度g,地球自转周期T,不考虑大气层对电磁波的影响且电磁波在空气中的传播速度为c)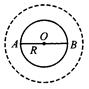
太阳的半径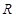 和地球半径
和地球半径 之比是110∶1,太阳的平均密度和地球的平均密度之比是1∶4,地球表面的重力加速度
之比是110∶1,太阳的平均密度和地球的平均密度之比是1∶4,地球表面的重力加速度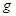 =9.8m/s2,试求太阳表面的重力加速度。
=9.8m/s2,试求太阳表面的重力加速度。
如图所示,一带电微粒质量为m=2.0×10-11kg、电荷量q=+1.0×10-5C,从静止开始经电压为U1=100V的电场加速后,水平进入两平行金属板间的偏转电场中,微粒射出电场时的偏转角θ=30º,并接着进入一个方向垂直纸面向里、宽度为D=34.6cm的匀强磁场区域。已知偏转电场中金属板长L=20cm,两板间距d=17.3cm,重力忽略不计。求:
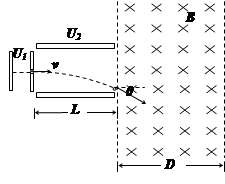
(1)带电微粒进入偏转电场时的速率v1
(2)偏转电场中两金属板间的电压U2
(3)为使带电微粒不会从磁场右边射出,该匀强磁场的磁感应强度B至少多大?
如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处。质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起。已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg。试问: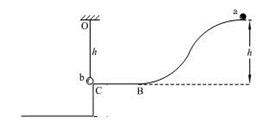
(1)a与b球碰前瞬间,a球的速度多大?
(2)a、b两球碰后,细绳是否会断裂?(要求通过计算回答)
如图所示,质量为m=50g的铜棒长L=10cm,用长度均为l,质量可不计的两根软导线水平地悬吊在竖直向上的匀强磁场B中,已知B=0.50T。通电后棒向纸外偏转,当棒处于静止状态时,悬线与竖直方向的夹角为q=37°。求铜棒中电流的方向及电流的大小.(取g=10m/s2,已知sin37°=0.6,cos37°=0.8) 
如图所示,一根长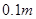 的细线,一端系着一个质量为
的细线,一端系着一个质量为 的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动,使小球的转速很缓慢地增加,当小球的角速度增加到开始时角速度的
的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动,使小球的转速很缓慢地增加,当小球的角速度增加到开始时角速度的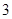 倍时,细线断开,线断开前的瞬间线受到的拉力比开始时大
倍时,细线断开,线断开前的瞬间线受到的拉力比开始时大 ,求:
,求: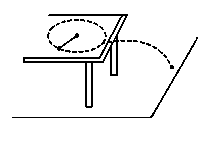
(1)线断开前的瞬间,线受到的拉力大小;
(2)线断开的瞬间,小球运动的线速度;
(3)如果小球离开桌面时,速度方向与桌边缘的夹角为 ,桌面高出地面
,桌面高出地面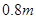 ,求小球飞出后的落地点距桌边缘的水平距离.
,求小球飞出后的落地点距桌边缘的水平距离.
在直径1.6m的圆柱体一端截出一圆锥,如下图所示,在看到剖面上,三角形的三边之比为3:4:5, 圆柱体可绕其中心对称轴匀速旋转。将一小木块放置在斜面的中点,它与斜面间动摩擦力因素为0.25,若小木块保持在此位置不动,则圆柱体旋转的角速度应为多大.(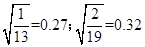 ;g取10m/s2)
;g取10m/s2)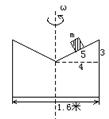
“嫦娥一号”探月卫星在环绕月球的极地轨道上运动,由于月球的自转,因而“嫦娥一号”卫星能探测到整个月球表面。2007年12月11日“嫦娥一号”卫星的CCD相机已对月球背面进行成像探测,并获得了月球背面部分区域的影像图。卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地公转的周期为TE,半径为R0;地球半径为RE,月球半径为RM。试解答下列问题: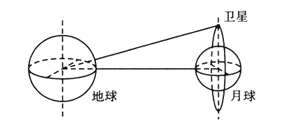
(1)若忽略地球及太阳引力对绕月卫星的影响,试求月球与地球的质量之比。
(2)若当绕月极地轨道的平面与月球绕地公转的轨道平面垂直,也与地心到月心的连线垂直(如图所示)时,探月卫星将向地球发送所拍摄的照片。已知光速为c,则此照片信号由探月卫星传送到地球最短需要多长时间?
质量为m=3000kg的汽车在水平公路上行驶,轮胎与路面间的最大静摩擦力为15000N,汽车经过半径为r=80m的弯路时,试问:
(1)如果汽车以速度v=36km/h沿弯路行驶,汽车的向心力为多大?是由什么力提供的?
(2)为保证汽车不发生侧滑,车速的最大值是多少?
将一物体以6m/s的速度从3.2m的高度水平抛出,球物体落地的速度。(g=10m/s2,sin53°=0.8,cos53°=0.6)
如图所示,ABC是光滑轨道,其中BC部分是半径为R的竖直放置的半圆.一质量为M的小木块放在轨道水平部分,木块被水平飞来的质量为m的子弹射中,并滞留在木块中.若被击中的木块沿轨道能滑到最高点C,已知木块对C点的压力大小为(M+m)g,求:子弹射入木块前瞬间速度的大小.
在光滑水平面上有一个静止的质量为M的木块,一颗质量为m的子弹以初速v0水平射入木块,且陷入木块的最大深度为d。设冲击过程中木块的运动位移为s,子弹所受阻力恒定。试证明:s<d。
质量为1kg的物体在倾角30º为的光滑斜面(固定)顶端由静止释放,斜面高5m,求物体从斜面顶端滑到物体的动量变化底端过程中重力的冲量为多少?物体的动量变化为多少?
分别用λ和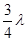 的单色光照射同一金属,发生的光电子的最大初动能之比为1∶2,以h表示普朗克常量,c表示真空中的光速,则此金属板的逸出功是多大?
的单色光照射同一金属,发生的光电子的最大初动能之比为1∶2,以h表示普朗克常量,c表示真空中的光速,则此金属板的逸出功是多大?
如图所示,倾角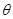 =30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1
=30°、宽度L=1m的足够长的U形平行光滑金属导轨固定在磁感应强度B=1T、范围充分大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行导轨的牵引力F,牵引一根质量m=0.2kg、电阻R=1 、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。问:
、垂直导轨的金属棒ab,由静止沿导轨向上移动(ab棒始终与导轨接触良好且垂直,不计导轨电阻及一切摩擦)。问:
(1)若牵引力为恒力,且F=9N,求金属棒达到的稳定速度v1
(2)若牵引力功率恒为72W,求金属棒达到的稳定速度v2
(3)若金属棒受向上拉力在斜面导轨上达到某一速度时,突然撤去力,此后金属棒又前进了0.48m ,从撤力至棒速为0的过程中,金属棒发热1.12J。问撤力时棒速v3多大?