高中物理α粒子散射实验计算题

(18分)如图所示，在坐标系xOy内有一半径为a的圆形区域，圆心坐标为O₁（a，0），圆内分布有垂直纸面向里的匀强磁场。在直线y＝a的上方和直线x＝2a的左侧区域内，有一沿y轴负方向的匀强电场，场强大小为E。一质量为m、电荷量为+q（q＞0）的粒子以速度v从O点垂直于磁场方向射入，当速度方向沿x轴正方向时，粒子恰好从O₁点正上方的A点射出磁场，不计粒子重力。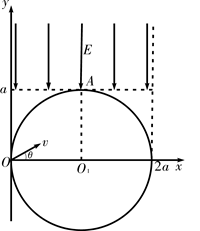

（1）求磁感应强度B的大小；
（2）粒子在第一象限内运动到最高点时的位置坐标；
（3）若粒子以速度v从O点垂直于磁场方向射入第一象限，当速度方向沿x轴正方向的夹角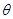=30°时，求粒子从射入磁场到最终离开磁场的时间t。

如图，直线MN 上方有平行于纸面且与MN成45^。的有界匀强电场，电场强度大小未知；MN下方为方向垂直于纸面向里的有界匀强磁场，磁感应强度大小为B。今从MN_上的O点向磁场中射入一个速度大小为v、方向与MN成45角的带正电粒子，该粒子在磁场中运动时的轨道半径为R。若该粒子从O点出发记为第一次经过直线MN，而第五次经过直线MN时恰好又通过O点。不计粒子的重力。求：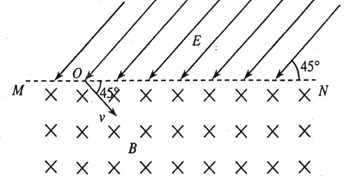

（1）电场强度的大小；
（2）该粒子从O点出发，第五次经过直线MN时又通过O点的时间；
（3）该粒子再次从O点进入磁场后，运动轨道的半径。

如图所示，带电平行金属板相距为2R，在两板间半径为R的圆形区域内有垂直纸面向里的匀强磁场，磁感应强度为B，两板及其左侧边缘连线均与磁场边界刚好相切。一带电粒子（不计重力）沿两板间中心线O₁O₂从左侧O₁点以某一速度射入，沿直线通过圆形磁场区域，然后恰好从极板边缘飞出，在极板间运动时间为t₀。若仅撤去磁场，质子仍从O₁点以相同速度射入，经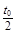时间打到极板上。求：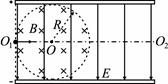

（1）两极板间电压U；
（2）若两极板不带电，保持磁场不变，带电粒子仍沿中心线O₁O₂从O₁点射入，欲使带电粒子从左侧飞出两板间，入射速度v应满足什么条件。

如图所示，y轴上A点距坐标原点的距离为L，坐标平面内有边界过A点和坐标原点O的圆形匀强磁场区域，磁场方向垂直坐标平面向里。有一电子（质量为m、电荷量为e）从A点以初速度v₀沿着x轴正方向射入磁场区域，并从x轴上的B点射出磁场区域，此时速度方向与x轴正方向之间的夹角为60°。求：

（1）磁场的磁感应强度大小；（2）电子在磁场中运动的时间。

如图所示，虚线OC与y轴的夹角θ=60°，在此角范围内有一方向垂直于xOy平面向外、磁感应强度大小为B的匀强磁场。一质量为m、电荷量为q的带正电的粒子a(不计重力)从y轴的点M（0，L）沿x 轴的正方向射入磁场中。求：

（1）要使粒子a离开磁场后垂直经过x轴，该粒子的初速度v₁为多大；
（2）若大量粒子a同时以v₂=从M点沿xOy平面的各个方向射入磁场中，则从OC边界最先射出的粒子与最后射出的粒子的时间差。

在半径为R的半圆形区域中有一匀强磁场，磁场的方向垂直于纸面，磁感应强度为B．一质量为m带有电量为q的粒子以一定的速度，沿垂直于半圆直径AD方向经P点（AP＝d）射入磁场（不计粒子重力影响）．

（1）如果粒子恰好从A点射出磁场，求入射粒子的速度v₁．
（2）如果粒子经纸面内Q点从磁场中射出，出射方向与半圆在Q点切线方向的夹角为φ（如图所示）．求入射粒子的速度v₂．

(12分)提纯氘核技术对于核能利用具有重大价值．下图是从质子、氘核混合物中将质子和氘核分离的原理图，x轴上方有垂直于纸面向外的匀强磁场，初速度为0的质子、氘核混合物经电压为U的电场加速后，从x轴上的A()点沿与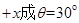的方向进入第二象限(速度方向与磁场方向垂直)，质子刚好从坐标原点离开磁场．已知质子、氘核的电荷量均为，质量分别为m、2m，忽略质子、氘核的重力及其相互作用．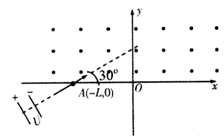

(1)求质子进入磁场时速度的大小；
(2)求质子与氘核在磁场中运动的时间之比；
(3)若在x轴上接收氘核，求接收器所在位置的横坐标．

在如图所示，x轴上方有一匀强磁场，磁感应强度的方向垂直于纸面向里，大小为B，x轴下方有一匀强电场，电场强度的大小为E，方向与y轴的夹角θ为45^o且斜向上方。现有一质量为m电量为q的正离子，以速度v₀由y轴上的A点沿y轴正方向射入磁场，该离子在磁场中运动一段时间后从x轴上的C点进入电场区域，该离子经C点时的速度方向与x轴夹角为45^o。 不计离子的重力，设磁场区域和电场区域足够大。求：

（1）C点的坐标；

（2）离子从A点出发到第三次穿越x轴时的运动时间；
（3）离子第四次穿越x轴时速度的大小及速度方向与电场方向的夹角.

如图所示，一个质量为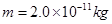，电荷量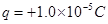的带电微粒（重力忽略不计），从静止开始经U₁＝100 V电压加速后，水平进入两平行金属板间的偏转电场，偏转电场的电压U₂＝100 V．金属板长L＝20cm，两板间距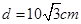。求：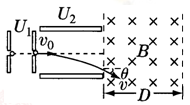

（1）微粒进入偏转电场时的速度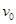大小；
（2）微粒射出偏转电场时的偏转角θ；
（3）若该匀强磁场的宽度为D＝10 cm，为使微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少多大？

如图在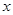轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场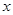，轴下方存在垂直纸面向外的磁感应强度为的匀强磁场。一带负电的粒子从原点O以与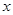轴成30°角的方向斜向上射入磁场，且在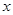轴上方运动半径为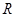。求：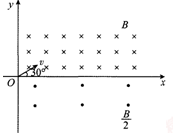

（1）粒子在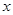轴下方磁场中运动的半径。
（2）粒子在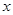轴下方磁场中运动的时间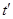与在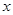轴上方磁场中运动的时间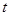之比。

如图所示，两块水平放置、相距为d的长金属板接在电压可调的电源上.两板之间的右侧区域存在方向垂直纸面向里的匀强磁场.将喷墨打印机的喷口靠近上板下表面，从喷口连续不断喷出质量均为m、水平速度均为v₀、带相等电荷量的墨滴.调节电源电压至U，墨滴在电场区域恰能沿水平向右做匀速直线运动；进入电场、磁场共存区域后，最后垂直打在下板的M点.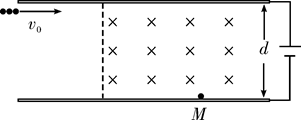

(1)判断墨滴所带电荷的种类，并求其电荷量；
(2)求磁感应强度B的值；
(3)现保持喷口方向不变，使其竖直下移到两板中间的位置.为了使墨滴仍能到达下板M点，应将磁感应强度调至B′，则B′的大小为多少？

如图所示，有一对平行金属板，两板相距为0.05m，电压为10V。两板之间有匀强磁场，磁感应强度大小为B₀=0.1T，方向与金属板面平行并垂直于纸面向里。图中右边有一半径R为0.1m、圆心为O的圆形区域内也存在匀强磁场，磁感应强度大小为，方向垂直于纸面向里。一正离子沿平行于金属板面，从A点垂直于磁场的方向射入平行金属板之间，沿直线射出平行金属板之间的区域，并沿直径CD方向射入圆形磁场区域，最后从圆形区域边界上的F点射出。已知速度的偏向角，不计离子重力。求：

（1）离子速度v的大小； （2）离子的比荷q/m； （3）离子在圆形磁场区域中运动时间t。

(12分)在如图所示的直角坐标系xoy中，矩形区域oabc内有垂直于纸面向外的匀强磁场，磁感应强度大小为B=5.0×10^-2T；第一象限内有沿-y方向的匀强电场，电场强度大小为E=1.0×10⁵N／C．已知矩形区域oa边长为0．60m，ab边长为0.20 m．在bc边中点N处有一放射源，某时刻，放射源沿纸面向磁场中各方向均匀地辐射出速率均为m/s的某种带正电粒子，带电粒子质量m=1.6×10^-27kg，电荷量为q=+3.2×10^-19kg，不计粒子重力，求：(计算结果保留两位有效数字)

(1)粒子在磁场中运动的半径；
(2)从x轴上射出的粒子中，在磁场中运动的最短路程为多少?
(3)放射源沿-x方向射出的粒子，从射出到从y轴离开所用的时间．

如图所示装置中，区域Ⅰ中有竖直向上的匀强电场，电场强度为E，区域Ⅱ内有垂直纸面向外的水平匀强磁场，磁感应强度为B。区域Ⅲ中有垂直纸面向里的水平匀强磁场，磁感应强度为2B。一质量为m、带电量为q的带负电粒子（不计重力）从左边界O点正上方的M点以速度v₀水平射入电场，经水平分界线OP上的A点与OP成60°角射入Ⅱ区域的磁场，并垂直竖直边界CD进入Ⅲ区域的匀强磁场中。求：

（1）粒子在Ⅱ区域匀强磁场中运动的轨道半径
（2）O、M间的距离
（3）粒子从M点出发到第二次通过CD边界所经历的时间

如图所示，在平面直角坐标系xOy中，第I象限存在沿y轴负方向的匀强电场，第IV象限存在垂直于坐标平面向外的匀强磁场，一带正电的粒子从y轴正半轴上的M点以速度v₀垂直于y轴射入电场，经偏转电场后到达x轴上的N点，然后射入磁场，最后从y轴负半轴上的P点垂直于y轴射出磁场，已知M点的坐标是（0,h）,N点的坐标是(2h,0),不计粒子重力，求：


（1）粒子到达N点时的速度v的大小以及v与初速度v₀的夹角；
（2）粒子在磁场中运动的轨道半径r；
（3）粒子从M点运动到P点的总时间t。