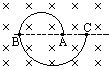如图21所示，第四象限内有互相正交的匀强电场E与匀强磁场B1，E的大小为1.5×103V／m，Bl大小为0.5T；第一象限的某个矩形区域内，有方向垂直纸面的匀强磁场B2，磁场的下边界与x轴重合。一质量m=1×10-14kg、电荷量q=2×l0-10C的带正电微粒以某一速度v沿与y轴正方
向60°角
从M点沿直线运动，经P点即进入处于第一象限内的磁场B2区域。一段时间后，小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为（0，-10），N点的坐标为（0，30），不计粒子重力，g取10m/s2。则求：
（1）微粒运动速度v的大小；
（2）匀强磁场B2的大小；
（3）B2磁场区域的最小面积。
如图所示，圆心在原点、半径为R的圆将xOy平面分为两个区域，在圆内区域Ⅰ（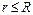
）和圆外区域Ⅱ（
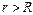）分别存在两个磁场方向均垂直于
平面的匀强磁场；垂直于平面放置了两块平面荧光屏，其中荧光屏甲平行于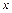
轴放置在
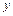轴坐标为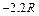
的位置，荧光屏乙平行于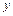轴放置在
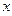轴坐标为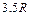
的位置。现有一束质量为
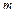、电荷量为
（
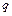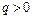）、动能为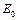
的粒子从坐标为（
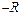，0）的
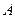点沿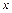轴正方向射入区域Ⅰ，最终打在荧光屏甲上，出现坐标为（
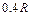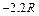，）的亮点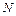
。若撤去圆外磁场，粒子打在荧光屏甲上，出现坐标为（
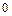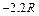，）的亮点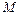
。此时，若将荧光屏甲沿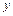轴负方向平移，则亮点的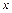轴坐标始终保持不变。（不计粒子重力影响）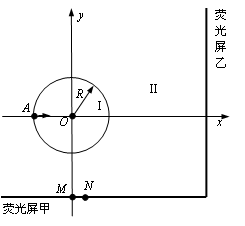
（1）求在区域Ⅰ和Ⅱ中粒子运动速度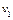
、
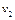的大小。
（2）求在区域Ⅰ和Ⅱ中磁感应强度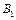
、
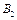的大小和方向。
（3）若上述两个磁场保持不变，荧光屏仍在初始位置，但从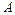
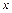点沿轴正方向射入区域Ⅰ的粒子束改为质量为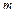、电荷量为
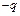、动能为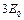
的粒子，求荧光屏上的亮点的位置。
三个速度大小不同而质量相同的一价离子，从长方形区域的匀强磁场上边缘平行于磁场边界射入磁场，它们从下边缘飞出时的速度方向如图所示。以下判断正确的是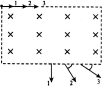
| A．三个离子均带负电 |
| B．三个离子均带正电 |
| C．离子1在磁场中运动的轨道半径最大 |
| D．离子3在磁场中运动的时间最长 |
真空中有一半径为r的圆柱形匀强磁场区域，磁场方向垂直
于纸面向里，Ox为过边界O点的切线，如图所示，从O点在纸面内向各个方向发射速率均为
的电子，设电子间相互作用忽略，且电子在磁场中的偏转半径也为r，已知电子的电荷量为e，质量为m。
⑴速度方向分别与Ox方向夹角成60°和90°的电子，在磁场中的运动时间分别为多少？
⑵所有从磁场边界射出的电子，速度方向有何特征？
⑶设在某一平面内有M、N两点，由M点向平面内各个方向发射速率均为的电子。请设计一种匀强磁场，使得由M点发出的所有电子都能够会聚到N点。
如图所示，在圆形区域内，存在垂直纸面向外的匀强磁场， ab是圆的一条直径。一带电粒子从a点射入磁场，速度大小为2v，方向与ab成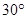
时恰好从b点飞出磁场，粒子在磁场中运动的时间为t；若仅将速度大小改为v，则粒子在磁场中运动的时间为（不计带电粒子所受重力）（ ）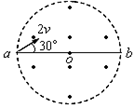
A． |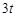
B． |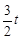
C． |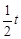
D．2t |
如图所示，MN是一荧光屏，当带电粒子打到荧光屏上时，荧光屏能够发光．MN的上方有磁感应强度为B的匀强磁场，磁场方向垂直纸面向里，P为屏上的一小孔，PQ与MN垂直．一群质量为m、带电荷量q的粒子（不计重力），以相同的速率v，从P点沿垂直于磁场方向射入磁场区域，其入射方向分布在以PQ为中心，夹角为2θ的范围内，不计粒子间的相互作用，以下说法正确的是（ ）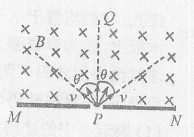
A．荧光屏上将出现一圆形亮斑，其半径为 |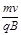
B．荧光屏上将出现一条亮线，其长度为 |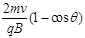
C．荧光屏上将出现一条亮线，其长度为 |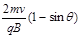
D．荧光屏上将出现一条亮线，其最右端距P点为 |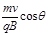
如图甲所示，带正电的粒子以水平速度v0从平行金属板MN间中线
连续射入电场中，MN板间接有如图乙所示的随时间t变化的电压
，电压变化周期T=0.1s，两板间电场可看做均匀的，且两板外无电场. 紧邻金属板右侧有垂直纸面向里的匀强磁场B，分界线为CD，AB为荧光屏. 金属板间距为d，长度为l，磁场B的宽度为d. 已知：
，带正电的粒子的比荷为q/m=108C/kg，重力忽略不计. 试求：
（1）带电粒子进入磁场做圆周运动的最小半径；
（2）带电粒子射出电场时的最大速度；
（3）带电粒子打在荧光屏AB上的范围.
如图所示，在第一象限内有垂直纸面向里的匀强磁场（磁场足够大），一对正、负电子分别以相同速度沿与x轴成300角的方向从原点垂直磁场射入，则负电子与正电子在磁场中运动时间之比为（不计正、负电子间的相互作用力）（ ）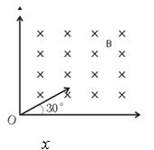
A．1： |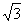
B．1：2 | C．1：1 | D．2：1 |
如图甲所示，在空间存在一个变化的电场和一个变化的磁场，电场的方向水平向右（图甲中由B到C），场强大小随时间变化情况如图乙所示；磁感应强度方向垂直于纸面、大小随时间变化情况如图丙所示。在t=ls时，从A点沿AB方向（垂直于BC）以初速度v0射出第一个粒子，并在此之后，每隔2s有一个相同的粒子沿AB方向均以初速度v0射出，并恰好均能击中C点，若AB=BC=l，且粒子由A运动到C的运动时间小于1s。不计空气阻力，对于各粒子由A运动到C的过程中，以下说法不正确的是 （ ）
A．第一个粒子和第二个粒子通过C的动能之比为1：5
B．第一个粒子和第二个粒子运动的加速度大小之比为1：2
C．第一个粒子和第二个粒子运动的时间之比为π:2
D．电场强度E0和磁感应强度B0的大小之比为3v0:l
如图所示，在半径为R的半圆形区域，有垂直于纸面的匀强磁场，磁感应强度为B。质量为m，带电荷量为q的微粒以某一初速度沿垂直于半圆直径AD方向从P点射入磁场，已知AP=d。不计空气阻力和微粒的重力。
（1）若微粒恰好从A点射出磁场，求微粒的入射速度v1；
（2）若微粒从纸面内的Q点射出磁场，且已知射出方向与半圆在Q点的切线成夹角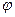
（如图），求微粒的入射速度v2。
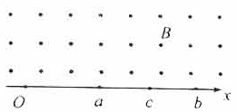
在轴上方有垂直于纸面的匀强磁场，同一种带电粒子从
点射入磁场。当入射方向与
轴的夹角
=" 45°" 时，速度为
、
的两个粒子分别从
、
两点射出磁场，如图所示，当
为60°时，为了使粒子从
的中点
射出磁场，则速度应为（）
| A． |
|
B． |
|
C． |
|
D． |
|
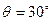
（1）若粒子恰好垂直于EC边射出磁场，求磁场的磁感应强度B为多少？
（2）改变磁感应强度的大小，粒子进入磁场偏转后能打到ED板，求粒子从进入磁场到第一次打到ED板的最长时间是多少？
（3）改变磁感应强度的大小，可以再延长粒子在磁场中的运动时间，求粒子在磁场中运动的极限时间。（不计粒子与ED板碰撞的作用时间。设粒子与ED板碰撞前后，电量保持不变并以相同的速率反弹）
如图所示，在垂直纸面向里的匀强磁场中，有一带电量为q的正离子自A点垂直射入磁场，沿半径为R的圆形轨道运动，运动半周到达B点时，由于吸收了附近若干静止的电子，沿另一个圆形轨道运动到BA的延长线上的C点，且AC的长度也为R．试求正离子在B点吸收的电量(不计重力)．
粤公网安备 44130202000953号