高中物理研究电磁感应现象计算题

如图所示，两条互相平行的光滑金属导轨位于水平面内，距离为l ＝0.2m，在导轨的一端接有阻值为R ＝ 0.5Ω的电阻，在X ≥ 0处有一与水平面垂直的均匀磁场，磁感强度B ＝ 0.5T。一质量为m ＝ 0.1kg的金属直杆垂直放置在导轨上，并以v0＝2m/s的初速度进人磁场，在安培力和一垂直于杆的水平外力 F的共同作用下作匀变速直线运动，加速度大小为a ＝ 2m/s2，方向与初速度方向相反。设导轨和金属杆的电阻都可以忽略，且接触良好，求：

（1）电流为零时金属杆所处的位置；
（2）电流为最大值的一半时施加在金属杆上外力 F的大小和方向；
（3）保持其他条件不变，而初速度v0取不同值，求开始时F方向与初速度v0取值关系

如图所示，两根平行金属导轨MN,PQ相距为d =1.0m，导轨平面与水平面夹角为a=300导轨上端跨接一定值电阻R=1.6Ω,导轨电阻不计。整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1T的匀强磁场中。金属棒ef垂直于MN、PQ静止放置，且与导轨保持良好接触,其长刚好也为d、质量m=0.1kg、电阻r=0.4Ω,距导轨底端s1=3.75m另一根与金属棒平行放置的绝缘棒gh长度也为d,质量为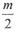，从轨道最低点以速度v0=10m/s沿轨道上滑并与金属棒发生正碰（碰撞时间极短），碰后金属棒沿导轨上滑s2=0.2m后再次静止，测得此过程中电阻R上产生的电热为Q=0.2J己知两棒与导轨间的动摩擦因数均为.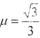，g取10m/s2,求：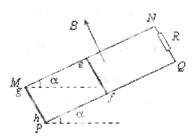

(1) 碰后瞬问两棒的速度；
(2) 碰后瞬间金属棒的加速度；
(3) 金属棒在导轨上运动的时间。

如图所示，足够长的光滑U形导体框架的宽度L =" 0.5" m，电阻忽略不计，其所在平面与水平面成角，磁感应强度B =" 0.8" T的匀强磁场方向垂直于导体框平面，一根质量m =" 0.2" kg，有效电阻R = 2Ω的导体棒MN垂直跨放在U形框架上，导体棒由静止开始沿框架下滑到刚开始匀速运动，通过导体棒截面的电量共为Q =" 2" C。求：

（1）导体棒匀速运动的速度；
（2）导体棒从开始下滑到刚开始匀速运动这一过程中，导体棒的电阻消耗的电功。（sin 37°=" 0.6 " cos 37°=" 0.8 " g = 10m/s2）

如图所示，面积为0.2 m2的100匝线圈处在匀强磁场中，磁场方向垂直于线圈平面.已知磁感应强度随时间变化的规律如图，定值电阻R1="6" Ω，线圈电阻R2="4" Ω，求：

（1）在图中标出流过R1的电流方向
(2) 回路中的感应电动势大小；

如图所示，一宽度为L的光滑金属导轨放置于竖直平面内，质量为m的金属棒ab沿金属导轨由静止开始保持水平自由下落，进入高h、方向垂直纸面向里、磁感应强度为B的匀强磁场区域。设金属棒与金属导轨始终保持良好接触，ab棒穿出磁场前已开始做匀速运动，且ab棒穿出磁场时的速度为进入磁场时速度的。已知ab棒最初距磁场上边界的距离为4h，定值电阻的阻值为R，棒及金属导轨电阻忽略不计，重力加速度为g。求：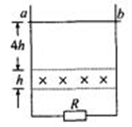

（1）ab棒刚进入磁场时通过电阻R的电流;
（2）在此过程中电阻R产生的热量Q的大小；
（3）金属棒穿出磁场时电阻R消耗的功率大小。

如图所示，边长L＝0.20m的正方形导线框ABCD由粗细均匀的同种材料制成，正方形导线框每边的电阻R0＝1.0Ω，金属棒MN与正方形导线框的对角线长度恰好相等，金属棒MN的电阻r＝0.20Ω. 导线框放置在匀强磁场中，磁场的磁感应强度B＝0.50T，方向垂直导线框所在平面向里．金属棒MN与导线框接触良好，且与导线框对角线BD垂直放置在导线框上，金属棒上的中点始终在BD连线上．若金属棒以v＝4.0m/s的速度向右匀速运动，当金属棒运动至AC位置时，求：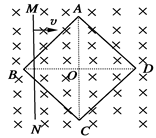

(1)金属棒产生的电动势大小；
(2)金属棒MN上通过的电流大小和方向；
(3)导线框消耗的电功率．

如图所示，小灯泡的规格为“2V、4W”，连接在光滑水平导轨上，两导轨相距0.1m，电阻不计，金属棒ab垂直搁置在导轨上，电阻1Ω，整个装置处于磁感强度B=1T的匀强磁场中，且磁场方向与导轨平面垂直.求：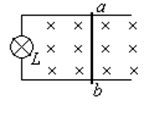

（1）为使小灯正常发光，ab的滑行速度多大？
（2）拉动金属棒ab的外力的功率多大？

如图14甲所示，光滑的平行水平金属导轨、相距，
在点和点间连接一个阻值为的电阻，在两导轨间矩形区域内有垂直导轨平面竖直向上、宽为的匀强磁场，磁感应强度为。一质量为、电阻为、长度也刚好为的导体棒垂直搁在导轨上，与磁场左边界相距。现用一个水平向右的力拉棒，使它由静止开始运动，棒离开磁场前已做匀速直线运动，棒与导轨始终保持良好接触，导轨电阻不计，随与初始位置的距离变化的情况如图14乙，已知。求：

（1）棒离开磁场右边界时的速度；
（2）棒通过磁场区域的过程中整个回路所消耗的电能；
（3）满足什么条件时，棒进入磁场后一直做匀速运动。

如图13所示，有一磁感强度的水平匀强磁场，垂直放置一很长的金属框架，框架上有一导体与框架边垂直且始终保持良好接触，由静止开始下滑。已知框架的宽度为，质量为，电阻为，框架电阻不计，取，求：

　　(1) 中电流的方向如何？
(2)导体下落的最大速度；
(3)导体在最大速度时的电功率。

如图，在相距为L的光滑的足够长的水平轨道上放有一金属杆AB，在光滑的倾斜轨道上放有另一个质量为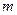的金属杆CD，金属杆与轨道接触良好，整个回路电阻为R，倾斜轨道与水平面夹角为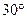。有一一个与水平轨道平面垂直、方向向下、磁感应强度为B1的匀强磁场；有另一个与倾斜轨道平面垂直、磁感应强度为B2的匀强磁场。为了使CD能够静止，金属杆船在外力F作用下向左匀速运动，试问：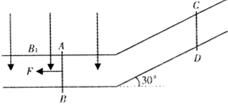

（1）匀强磁场B2的方向；
（2）通过CD杆的电流大小；
（3）外力F的功率是多大?

如图甲所示，质量m=6.0×10-3kg，边长L=0.20m，电阻R=1.0欧的正方形单匝金属线框abcd，置于倾角30°的绝缘斜面上，ab边沿着水平方向，线框的下半部分处于垂直斜面向上的匀强磁场中，磁感应强度B随时间t按图乙所示的规律周期性变化，线框在斜面上始终保持静止，g=10,求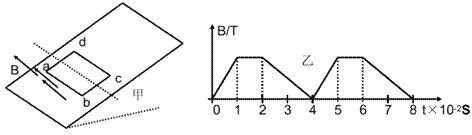

（1）在2.0×10-2s~4.0×10-2s时间内线框中产生感应电流的大小
（2）在t=3.0×10-2s时间内线框受到斜面的摩擦力的大小和方向。
（3）一个周期内感应电流在线框中产生的平均电功率

一电阻为R的金属圆环，放在匀强磁场中，磁场与圆环所在平面垂直，如图(a)，已知通过圆环的磁通量随时间t的变化关系如图(b），图中的最大磁通量和变化周期T都是已知量，求：

(1)在t=0到t= T/4的时间内，通过金属圆环横截面的电荷量q
(2)在t=0到t=2T的时间内，金属环所产生的电热Q

如图甲所示，一对平行光滑轨道放置在水平面上，两轨道间距l＝0.20 m，电阻R＝1.0 Ω.有一导体杆静止地放在轨道上，与两轨道垂直，杆及轨道的电阻皆可忽略不计，整个装置处于磁感应强度B＝0.50 T的匀强磁场中，磁场方向垂直轨道面向下．现用一外力F沿轨道方向拉杆，使之做匀加速运动，测得力F与时间t的关系如图乙所示．求出杆的质量m和加速度a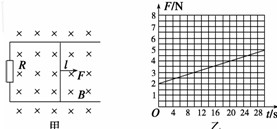

一光滑金属导轨如图所示，水平平行导轨MN、ST相距＝0.5m，竖直半圆轨道NP、TQ直径
均为 D＝0.8m，轨道左端用阻值R＝0.4Ω的电阻相连．水平导轨的某处有一竖直向上、磁感应强度B＝0.06T的匀强磁场．光滑金属杆ab质量m＝0.2kg、电阻r＝0.1Ω，当它以5m/s的初速度沿水平导轨从左端冲入磁场后恰好能到达竖直半圆轨道的最高点P、Q．设金属杆ab与轨道接触良好，并始终与导轨垂直，导轨电阻忽略不计．取g＝10m/s²，求金属杆：
（1）刚进入磁场时，通过金属杆的电流大小和方向；
（2）到达P、Q时的速度大小；
（3）冲入磁场至到达P、Q点的过程中，电路中产生的焦耳热．

如图所示，两根不计电阻的金属导线MN与PQ放在水平面内，MN是直导线，PQ的PQ₁段是直导线，Q₁Q₂段是弧形导线，Q₂Q₃段是直导线，MN、PQ₁、Q₂Q₃相互平行，M、P间接入一个阻值R=0.25Ω的电阻。一根质量为1.0 kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动，金属棒始终垂直于MN，整个装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向竖直向下。金属棒处于位置（I）时，给金属棒一个向右的速度v₁=4 m/s，同时方向水平向右的外力F₁ ="3" N作用在金属棒上使金属棒向右做匀减速直线运动；当金属棒运动到位置(Ⅱ)时，外力方向不变，大小变为F₂，金属棒向右做匀速直线运动，经过时间t ="2" s到达位置(Ⅲ)。金属棒在位置(I)时，与MN、Q₁Q₂相接触于a、b两点，a、b的间距L₁=1 m，金属棒在位置(Ⅱ)时，棒与MN、Q₁Q₂相接触于c、d两点。已知s₁="7.5" m。求：（1）金属棒向右匀减速运动时的加速度大小?
（2）c、d两点间的距离L₂=?
（3）外力F₂的大小？
（4）金属棒从位置(I)运动到位置(Ⅲ)的过程中，电阻R上放出的热量Q=？