高中物理电学实验试题

如图所示，一个均匀的带电圆环，带电量为+Q，半径为R，放在绝缘水平桌面上。圆心为O点，放O点做一竖直线，在此线上取一点A，使A到O点的距离为R，在A点放一检验电荷+q，则+q在A点所受的电场力为（   ）

A．，方向向上	B．，方向向上
C．，方向水平向左	D．不能确定

如图所示，理想变压器的副线圈上通过输电线接有三只灯泡L₁、L₂和L₃，输电线的等效电阻为R，原线圈接有一个理想的电流表，电源电压大小不变．开始时开关S接通，当S断开时，以下说法正确的是（  ）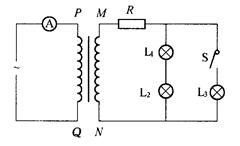

A．原线圈两端P、Q间的输入电压减小

B．等效电阻R上消耗的功率变大

C．原线圈中电流表示数变小

D．灯泡L1和L2变亮

如图所示，A、B两个带电小球的质量均为m，所带电量分别为+q和－q，两球间用绝缘细线连接，A球又用绝缘细线悬挂在天花板上，细线长均为L。现在两球所在的空间加上一方向向左的匀强电场，电场强度，由于有空气阻力，A、B两球最后会达到新的平衡位置，则在这个过程中，两个小球

A．总重力势能增加了   B．总重力势能增加了
C．总电势能减少了     D．总电势能减少了

某理想变压器的原、副线圈按如图所示电路连接，图中电表均为理想交流电表，且R₁=R₂，电键S原来闭合。现将S断开，则电压表的示数U、电流表的示数I、电阻R₁上的功率P₁、变压器原线圈的输入功率P的变化情况分别是

A．U增大	B．I增大
C．P1减小	D．P增大

一块电流表的内阻大约是几百欧，某同学用如图所示的电路测量其内阻和满偏电流，部分实验步骤如下：

①选择器材：两个电阻箱、2节干电池（每节电动势为1.5V，内阻不计）、2个单刀单掷开关和若干导线；
②按如图所示的电路图连接好器材，断开开关S₁、S₂，将电阻箱1的电阻调至最大；
③闭合开关S₁，调节电阻箱1，并同时观察电流表指针，当指针处于满偏刻度时，读取电阻箱1的阻值为500 Ω；
④保持电阻箱1的电阻不变，再闭合开关S₂，只调节电阻箱2，并同时观测电流表指针，当指针处于半偏刻度时，读取电阻箱2的阻值为250 Ω。
通过分析与计算可知：
（1）电流表内阻的测量值R_A＝__________；电流表的满偏电流值I_g＝__________；
（2）该同学对此电流表进行改装，使改装后的电流表量程为3 A，则改装后的电流表的内阻＝__________。

某理想变压器原、副线圈匝数比为55∶9，原线圈输入电压按图3所示的规律变化，副线圈接有负载。则

A．变压器输入、输出电流之比为55∶9

B．变压器输入、输出功率之比为55∶9

C．变压器输出电压的有效值为36V

D．变压器输出电压的频率为2×10^-2Hz

(18分)1897年汤姆逊发现电子后，许多科学家为测量电子的电荷量做了大量的探索。1907-1916年密立根用带电油滴进行实验，发现油滴所带的电荷量是某一数值的整数倍，于是称这数值为基本电荷。
如图所示，完全相同的两块金属板正对着水平放置，板间距离为。当质量为的微小带电油滴在两板间运动时，所受空气阻力的大小与速度大小成正比。两板间不加电压时，可以观察到油滴竖直向下做匀速运动，通过某一段距离所用时间为；当两板间加电压(上极板的电势高)时，可以观察到同一油滴竖直向上做匀速运动，且在时间内运动的距离与在时间内运动的距离相等。忽略空气浮力。重力加速度为。

（1）判断上述油滴的电性，要求说明理由；
（2）求上述油滴所带的电荷量；
（3）在极板间照射X射线可以改变油滴的带电量。再采用上述方法测量油滴的电荷量。如此重复操作，测量出油滴的电荷量如下表所示。如果存在基本电荷，请根据现有数据求出基本电荷的电荷量(保留到小数点后两位)。

实验次序	1	2	3	4	5
电荷量	0.95	1.10	1.41	1.57	2.02

两块水平放置的金属板间的距离为d，用导线与一个多匝线圈相连，线圈电阻为r，线圈中有竖直方向均匀变化的磁场，其磁通量的变化率为k，电阻R与金属板连接，如图所示。两板间有一个质量为m，电荷量为+q的油滴恰好处于静止状态，重力加速度为g，则线圈中的磁感应强度B的变化情况和线圈的匝数n分别为（   ）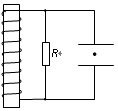

A．磁感应强度B竖直向上且正在增强，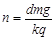

B．磁感应强度B竖直向下且正在增强，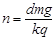

C．磁感应强度B竖直向上且正在减弱，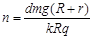

D．磁感应强度B竖直向下且正在减弱，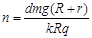

霓虹灯的激发电压和熄灭电压均为U₀=50V，现有一正弦交流电源U=20sin10tV.为了使霓虹灯能够正常工作利用一个升压变压器，匝数比为1：5，如图所示，则下列说法正确的是                                     （   ）

A．电压表读数为100V

B．霓虹灯在1秒钟内闪亮100次

C．霓虹灯闪亮一次持续时间为0.005秒

D．霓虹灯两端的交流电压的有效值为50V

在如图所示的空间里，存在垂直纸面向里的匀强磁场，磁感应强度为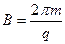。在竖直方向存在交替变化的匀强电场（竖直向上为正），电场大小为。一倾角为θ、长度足够的光滑绝缘斜面放置在此空间。斜面上有一质量为m，带电量为－q的小球，从t=0时刻由静止开始沿斜面下滑，设第1秒内小球不会离开斜面，重力加速度为g。求：
（1）第1秒末小球的速度。
（2）第2秒内小球离开斜面的最大距离。
（3）若假设第5秒内小球未离开斜面，θ角应满足什么条件？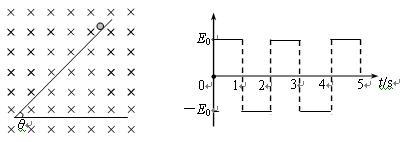

如图所示，理想变压器原线圈通入交流电流,副线圈接有一电流表，与负载电阻串联，电流表的读数为，在时，原线圈中电流的瞬时值为0．03，由此可知该变压器的原、副线圈的匝数比为

A．

B．

C．

D．

如图所示，光滑绝缘水平面上有甲、乙两个带电小球（可视为点电荷）。t=0时，乙电荷向甲运动，速度为6m/s，甲的速度为0。此后，它们仅在相互静电力的作用下沿同一直线运动（整个运动过程中没有接触），它们运动的速度（v）一时间（t）图象分别如图中甲、乙两曲线所示．则由图线可知（      ）

A．甲、乙两小球一定带同种电荷

B．t1时刻两电荷的电势能最大

C．0~t2时间内两电荷间的相互作用力一直增大

D．t1~t3时间内，乙的动能一直减小

(14分)如图所示，电荷量均为q，质量分别为m和2m的小球A和B，中间有细线相连。在电场中以v₀匀速上升。某时刻细线断开，求：（1）电场强度的大小；（2）当B球速度为零时，小球A的速度大小；（3）自绳子断开到B球速度为零的过程中，两球机械能的增量。

如图所示，在竖直放置的光滑半圆形绝缘细管的圆心O处放一点电荷。现将质量为m、电荷量为q的小球从半圆形管的水平直径端点A静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力。若小球所带电量很小，不影响O点处的点电荷的电场，则置于圆心处的点电荷在B点处的电场强度的大小为（       ）

A．	B．
C．	D．

图中虚线MN是一垂直纸面的平面与纸面的交线，在平面右侧的半空间存在一磁感强度为B的匀强磁场，方向垂直纸面向外。O是MN上的一点，从O点可以向磁场区域发射电量为+q、质量为m、速率为v的粒子，粒子射入磁场时的速度可在纸面内各个方向。已知先后射入的两个粒子恰好在磁场中给定的P点相遇，P到O的距离为L。不计重力及粒子间的相互作用。
(1)求所考察的粒子在磁场中的轨道半径。
(2)求这两个粒子从O点射入磁场的时间间隔。