如图,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为L,b与转轴的距离为2L。木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )

| A.b一定比a先开始滑动 |
| B.a、b所受的摩擦力始终相等 |
C.ω= 是b开始滑动的临界角速度 是b开始滑动的临界角速度 |
D.当ω= 时,a所受摩擦力的大小为kmg 时,a所受摩擦力的大小为kmg |
长为L的轻绳一端系一质量为m的物体,另一端被质量为M的人用手握住,人站在水平地面上,使物体在竖直平面内作圆周运动,物体经过最高点时速度为v,此是夫对地面的压力为( )
A. |
B.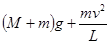 |
C. |
D.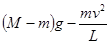 |
如图所示,汽车通过拱形桥时的运动可看做圆周运动.质量为m的汽车以速率v过桥,若桥面的圆弧半径为R,重力加速度为g,则汽车通过桥面最高点时对桥面的压力大小为( )

| A.mg | B. |
C.mg- |
D.mg+  |
如图所示,AB是位于竖直平面内、半径R=0.5 m的 圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103 N/C.今有一质量为m=0.1 kg、带电荷量q=+8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10 m/s2,求:
圆弧形的光滑绝缘轨道,其下端点B与水平绝缘轨道平滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=5×103 N/C.今有一质量为m=0.1 kg、带电荷量q=+8×10-5C的小滑块(可视为质点)从A点由静止释放.若已知滑块与水平轨道间的动摩擦因数μ=0.05,取g=10 m/s2,求:
(1) 小滑块第一次经过圆弧形轨道最低点B时对B点的压力;
(2) 小滑块运动到右侧最远处到最低点B的距离;
(3) 小滑块在水平轨道上通过的总路程。
如图所示,光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接.在过圆心O的水平界面MN的下方分布有水平向右的匀强电场.现有一质量为m,电量为+q的小球从水平轨道上A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方.小球可视为质点,小球运动到C点之前电量保持不变,经过C点后电量立即变为零).已知A、B间距离为2R,重力加速度为g.在上述运动过程中,( )

A.小球经过C点时的速度大小为
B.电场强度大小E=
C.小球经过B点时动能最大
D.小球的最大动能为mgR(1+ )
)
如图,在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道,水平轨道的PQ段铺设特殊材料,调节其初始长度为l,水平轨道左侧有一轻质弹簧左端固定,弹簧处于自然伸长状态.可视为质点的小物块从轨道右侧A点以初速度v0冲上轨道,通过圆形轨道、水平轨道后压缩弹簧,并被弹簧以原速率弹回.已知R=0.4m,l=2.5m,v0=6m/s,物块质量m=1kg,与PQ段间的动摩擦因数μ=0.4,轨道其它部分摩擦不计.取g=10m/s2.求: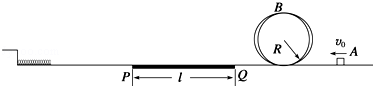
(1)物块经过圆轨道最高点B时对轨道的压力;
(2)物块从Q运动到P的时间及弹簧获得的最大弹性势能;
(3)物块仍以v0从右侧冲上轨道,调节PQ段的长度l,当l长度是多少时,物块恰能不脱离轨道返回A点继续向右运动.
质量为m的小球在竖直平面内的圆形轨道的内侧运动,经过最高点而不脱离轨道的临界速度为 ,当小球以2
,当小球以2 的速度经过最高点时,对轨道的压力大小是( )
的速度经过最高点时,对轨道的压力大小是( )
| A.0 | B.mg | C.3mg | D.5mg |
如图所示,在第Ⅱ象限内有水平向右的匀强电场,电场强度为E,在第Ⅰ、Ⅳ象限内分别存在如图所示的匀强磁场,磁感应强度大小相等,有一个带电粒子以垂直于x轴的初速度v0从x轴上的P点进入匀强电场中,并且恰好与y轴的正方向成45°角进入磁场,又恰好垂直x轴进入第Ⅳ象限的磁场,已知OP之间的距离为d,(不计粒子重力)求:
(1)带电粒子在磁场中做圆周运动的半径;
(2)带电粒子从进入磁场到第二次经过x轴,在磁场中运动的总时间;
(3)匀强磁场的磁感应强度大小。
如图所示,在竖直平面内,由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的光滑轨道,AB与BC的连接处是半径很小的圆弧,BC与CD相切,圆形轨道CD的半径为R。质量为m的小物块从倾斜轨道上距水平面高为h=3R处由静止开始下滑。求:
(1)小物块通过B点时速度vB的大小;
(2)试通过计算说明,小物块能否通过圆形轨道的最高点D。
一个质量为m电荷量为q的带电粒子从x轴上的P(a,0)点以速度v,沿与x正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限,不计重力.求:
(1)粒子做圆周运动的半径R
(2)匀强磁场的磁感应强度B.
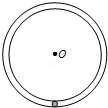
如图所示为空间站中模拟地球上重力的装置.环形实验装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体与在地球表面处有同样的“重力”,则旋转角速度应为(地球表面重力加速度为g,装置的外半径为R)( )
A. |
B. |
C.2 |
D. |
如图所示,倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切,切点为B,整个轨道处在竖直平面内.一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑并进入圆环轨道.接着小滑块从圆环最高点C水平飞出,恰好击中导轨上与圆心O等高的P点,不计空气阻力.求:
(1)滑块运动到圆环最高点C时的速度的大小;
(2)滑块运动到圆环最低点时对圆环轨道压力的大小;
(3)滑块在斜面轨道BD间运动的过程中克服摩擦力做的功。
某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点的速度的实验,所用器材有:玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20m)。完成下列填空:
将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为1.00kg;
将玩具车静置于凹形桥模拟器最低点时,托盘秤的示数如图b所示,该示数为______kg;
将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m;多次从同一位置释放小车,记录各次的m值如下表所示:
| 序号 |
1 |
2 |
3 |
4 |
5 |
| m(kg) |
1.80 |
1.75 |
1.85 |
1.75 |
1.90 |
根据以上数据,可求出小车经过凹形桥最低点时对桥的压力为____N;小车通过最低点时的速度大小为______m/s。(重力加速度 ,计算结果保留2位有效数字)。
,计算结果保留2位有效数字)。
如图所示,ABCD竖直放置的光滑绝缘细管道,其中AB部分是半径为R的 圆弧形管道,BCD部分是固定的水平管道,两部分管道恰好相切于B。水平面内的M、N、B三点连线构成边长为L等边三角形,MN连线过C点且垂直于BCD。两个带等量异种电荷的点电荷分别固定在M、N两点,电荷量分别为
圆弧形管道,BCD部分是固定的水平管道,两部分管道恰好相切于B。水平面内的M、N、B三点连线构成边长为L等边三角形,MN连线过C点且垂直于BCD。两个带等量异种电荷的点电荷分别固定在M、N两点,电荷量分别为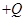 和
和 。现把质量为
。现把质量为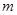 、电荷量为
、电荷量为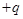 的小球(小球直径略小于管道内径,小球可视为点电荷),由管道的A处静止释放,已知静电力常量为
的小球(小球直径略小于管道内径,小球可视为点电荷),由管道的A处静止释放,已知静电力常量为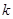 ,重力加速度为
,重力加速度为 。求:
。求: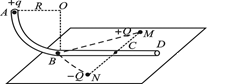
(1)小球运动到B处时受到电场力的大小;
(2)小球运动到C处时的速度大小;
(3)小球运动到圆弧最低点B处时,小球对管道压力的大小。