如图所示,细绳一端系着质量M=0.6 kg的物体,静止于水平面上,另一端通过光滑小孔吊着质量m=0.3 kg的物体,M的中点与圆孔距离为0.2 m,并知M和水平面的最大静摩擦力为2 N.现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(g取10 m/s2)
有一根长为2L的轻质细线,它的两端固定在一根长为L的竖直转轴AB上,线上套一个可以自由移动的质量为m的小球.当转轴转动时,小球正好以B为圆心,在水平面内做匀速圆周运动.求细线的张力和小球的线速度.
如图所示,用细绳系着一个小球,使小球在水平面内做匀速圆周运动,不计空气阻力,关于小球受力说法正确的是 ( )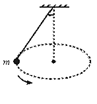
| A.只受重力 | B.只受拉力 |
| C.受重力、拉力和向心力 | D.受重力和拉力 |
如图所示,轻杆长为3L, 在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑水平转动轴上,杆和球在竖直面内转动,已知球A运动到最高点时,球A对杆恰好无作用力。求: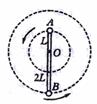
(1)球A在最高点时的角速度大小;
(2)球A在最高点时,杆对水平轴的作用力的大小和方向。
长度L=0.4m的细线,拴着一个质量m=0.3kg的小球,在竖直平面内作圆周运动,小球运动到最低点时离地面高度h=0.8m,此时细线受到的拉力F=7N,g取10m/s2,求:
(1)小球在最低点速度的大小;
(2)若小球运动到最低点时细线恰好断裂,则小球着地时速度为多大?
圆形光滑轨道位于竖直平面内,其半径为R,质量为m的金属小环套在轨道上,并能自由滑动,如图所示,以下说法正确的是 ( )
A.要使小环能通过轨道的最高点,小环通过最低点时的速度必须大于 |
B.要使小环能通过轨道的最高点,小环通过最低时的速度必须大于 |
C.如果小圆环在轨道最高点时的速度等于 ,则小环挤压轨道内侧 ,则小环挤压轨道内侧 |
D.如果小圆环在轨道最高点时的速度小于 ,则小环挤压轨道外侧 ,则小环挤压轨道外侧 |
质量为m的小球在竖直平面内的圆形轨道内侧运动,若经最高点不脱离轨道的临界速度为v,则当小球以2v速度经过最高点时,小球对轨道压力的大小为
| A.0 | B.mg | C.3mg | D.5mg |
如图所示,在竖直的转动轴上,a、b两点间距为40 cm,细线bc长30 cm, ac长50 cm,在c点系一质量为m的小球,在转动轴带着小球转动过程中,下列说法不正确的是
| A.转速小时,ac受拉力,bc松弛 |
| B.bc刚好拉直时,ac中拉力为1.25mg |
| C.bc拉直后转速增大,ac拉力不变 |
| D.bc拉直后转速增大,ac拉力增大 |
长度为L=0.3m的轻质细杆OA,A端有一质量为m=0.3kg的小球,如图下所示,小球以O点为圆心,在竖直平面内做圆周运动,通过最高点时,杆对小球的弹力是FN=1N,g取10 m/s2,则小球此时的速度可能为
| A.3m/s | B. m/s m/s |
C.2m/s | D. m/s m/s |
下列关于向心加速度的说法中,正确的是
| A.向心加速度的方向始终与速度的方向垂直 |
| B.向心加速度的方向保持不变 |
| C.在匀速圆周运动中,向心加速度是恒定的 |
| D.在匀速圆周运动中,线速度是恒定的 |
滚轴溜冰运动是青少年喜爱的一项活动。如图14所示,一滚轴溜冰运动员(可视为质点)质量m=30kg,他在左侧平台上滑行一段距离后沿水平飞出,恰能无能量损失地从A点沿切线方向进入竖直圆弧轨道并沿轨道下滑,且到达轨道最低点O时的速率是刚进入圆弧轨道时的1.2倍。已知A、B为圆弧的两端点,其连线水平;圆弧半径R="1.0" m,图中运动员进入圆弧轨道时对应速度v与水平方向AB连线的夹角θ=53º;左侧平台与A、B连线的高度差h="0.8" m。(取sin53º=0.80,cos53º=0.60),求:
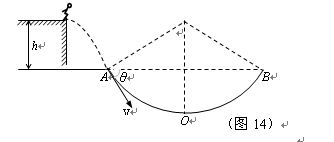
(1)运动员做平抛运动的初速度;
(2)运动员运动到圆弧轨道最低点O时,对轨道的压力。
一辆在水平公路上行驶的汽车,质量m=2.0×103kg,轮胎与路面间的最大静摩擦力fm=7.5×103N。当汽车经过一段半径R=60m的水平弯路时,为了确保不会发生侧滑,汽车转弯时的行驶速率不得超过多少?为保证汽车能安全通过弯路,请你对公路及相应设施的设计,提出合理化建议。
一个半径为R=0.5m的水平转盘可以绕竖直轴O’O’’转动,水平转盘中心O’处有一个光滑小孔,用一根长L=1m细线穿过小孔将质量分别为200g和500g小球A和小物块B连接,小物块B 放在水平转盘的边缘且与转盘保持相对静止,如图所示。现让小球A在水平面做角速度ωA=" 5" rad/s的匀速圆周运动,小物块B与水平转盘间的动摩擦因素μ="0.3" (取g="10" m/s2),求:
(1)细线与竖直方向的夹角θ;
(2)小物块B与水平转盘间要保持相对静止,水平转盘角速度ωB的取值范围;