如右图甲所示，有一质量为m、带电量为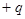
的小球在竖直平面内做单摆，摆长为L，当地的重力加速度为
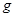，则周期
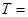；若在悬点处放一带正电的小球（图乙），则周期将 。（填“变大”、“不变”、“变小”）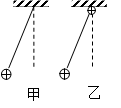
如图所示，半径是0.2m的圆弧状光滑轨道置于竖直面内并固定在地面上，轨道的最低点为B，在轨道的A点（弧AB所对圆心角小于5°）和弧形轨道的圆心O两处各有一个静止的小球Ⅰ和Ⅱ，若将它们同时无初速释放，先到达B点的是________球
已知地面重力加速度大约是月面重力加速度的6倍。那么一台地面上的秒摆（运动周期为2.0秒）在月面上的运动周期约为 秒。（结果保留两位有效数字）
一个单摆在甲地时，在时间t内完成m次全振动，移至乙地时，经过相同的时间完成n次全振动，则甲、乙两地重力加速度大小之比g甲：g乙等于______________。
如图所示，半径是0.2m的圆弧状光滑轨道置于竖直面内并固定在地面上，轨道的最低点为B，在轨道的A点（弧AB所对圆心角小于5°）和弧形轨道的圆心O两处各有一个静止的小球Ⅰ和Ⅱ，若将它们同时无初速释放，先到达B点的是________球
几名学生进行野外考察，登上一山峰后，他们想粗略测出山顶处的重力加速度。于是他们用细线拴好石块P系在树枝上做成一个简易单摆，如图所示。然后用随身携带的钢卷尺、电子手表进行了测量。同学们首先测出摆长L，然后将石块拉开一个小角度，由静止释放，使石块在竖直平面内摆动，用电子手表测出单摆完成n次全振动所用的时间t。
①利用测量数据计算山顶处重力加速度的表达式g= ；
②若振动周期测量正确，但由于难以确定石块重心，测量摆长时从悬点一直量到石块下端，所以用这次测量数据计算出来的山顶处重力加速度值比真实值 （选填“偏大”、“偏小”或“相等”）。
利用单摆测重力加速度时， 没有测摆球的直径， 先用直尺测出悬点到球底的距离L1， 测出相应的周期T1， 再将L1改变为L2， 又测出相应的周期T2， 则测出的重力加速度g的表达式应为 ．
在“用单摆测重力加速度”的实验中，某同学发现单摆的摆角（即单摆偏离平衡位置的最大角度）逐渐减小。一次测量中，他使用摆长为0.960m的单摆，如图所示。摆球从摆角θ<5°开始振动，某次当摆球从A到B经过平衡位置O时开始计时，发现该单摆随后经过30次全振动的总时间是59.6s，经过50次全振动停止在平衡位置。该同学测得当地的重力加速度值约为________m/s2；由于空气阻力的影响，该同学测得的重力加速度值_________（选填“偏大”、“偏小”或“不变”）。
如图所示的单摆，摆球a向右摆动到最低点时，恰好与一沿水平方向向左运动的粘性小球b发生碰撞，并粘接在一起，且摆动平面不变。已知碰撞前a球摆动的最高点与最低点的高度差为h，偏角θ较小，摆动的周期为T，a球质量是b球质量的4倍，碰撞前a球在最低点的速度是b球速度的一半。则碰撞后，摆动的周期为_________T，摆球的最高点与最低点的高度差为_________ h。
一个单摆的振动周期为T。若只将摆长缩为原来的
时，周期为 ；若只将摆球质量减为原来的时，周期为 ；若只将振幅减为原来的时，周期为 。
如图所示的单摆，摆球a向右摆动到最低点时，恰好与一沿水平方向向左运动的粘性小球b发生碰撞，并粘接在一起，且摆动平面不变。已知碰撞前a球摆动的最高点与最低点的高度差为h，偏角θ较小，摆动的周期为T，a球质量是b球质量的4倍，碰撞前a球在最低点的速度是b球速度的一半。则碰撞后，摆动的周期为_________T，摆球的最高点与最低点的高度差为_________ h。 
（1）在探究单摆周期与摆长关系的实验中，有如下器材供选用，请把应选器材的字母填在括号中（ ）
| A．1 m长的粗绳 | B．1 m长的细绳 | C．时钟 | D．秒表E、半径为1cm的小木球 |
F、半径为1cm的小铅球 G、米尺I、铁架台J、天平、H、砝码
（2）用 来测摆线长度。加上小球的半径得到摆长。用 计时。测量50次全振动的时间，来计算周期。计时应从 位置开始。
粤公网安备 44130202000953号
