高中物理力学实验试题

如图所示，质量M=10kg的木楔静止于粗糙水平地面上，木楔与地面间的动摩擦因数，在木楔的倾角为的斜面上，有一质量m=1.0kg的物块由静止开始沿斜面下滑，当滑行路程s=1.4m时，其速度v=1.4m/s.在这个过程中木楔处于静止状态.求地面对木楔的摩擦力的大小和方向（取g=10m/s²）.                    

某学习小组通过实验知道：在弹性限度内，弹簧的弹力F 的大小与弹簧的伸长（或缩短）量x 成正比，公式表达为F=kx；并且不同的弹簧，其劲度系数k也不同．现在该学习小组将两根已知劲度系数分别为k_l、k₂的弹簧A和B串接成一根新弹簧，并想通过实验确定新弹簧的劲度系数k₃与k_l、k₂的关系．
(1)甲同学猜想是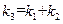，乙同学猜想是。其中有一位同学的猜想是对的，请你判断出谁对谁错，并写出判断依据．
____________________________________________________________________________。
(2)为了验证理论推导的正确性，可通过实验来完成．实验所需的器材除了弹簧A 和B、已
知质量m且质量相等的钩码外，还需要的器材有_______________________________。
(3)请你写出完整的实验步骤．

拧开水龙头水就会流出来，为什么连续的水流柱的直径在下流过程中会变小？设水龙头的开口直径为1cm，安装在离地面75cm高处，若水龙头开口处水的流速为1m/s，那么水流柱落到地面的直径应为多少？[6]

从匀速上升的直升飞机上落下一个物体，以下说法中正确的是（    ）[2]

A．从地面上看，物体做自由落体运动

B．从飞机上看，物体做竖直上抛运动

C．物体和飞机之间的距离开始减小，后来增大

D．物体落地时的速度一定大于匀速上升的飞机的速度

一石块A从80m高的地方自由下落，同时在地面正对着这石块，用40 m/s的速度竖直向上抛出另一石块B，问：（g="10" m/s²）
⑴石块A相对B是什么性质的运动？
⑵经多长时间两石块相遇？
⑶相遇时离地面有多高？[3]

一只球从高处自由下落，下落0.5s时，一颗子弹从其正上方向下射击，要使球在下落1.8m时被击中，则子弹发射的初速度为多大？（g="10" m/s²）[4]

在绳的上、下两端各拴着一小球，一人用手拿住绳上端的小球站在三层楼的阳台上，放手后小球自由下落，两小球落地的时间差为，如果人站在四层楼的阳台上，放手让其自由下落，两小球落地的时间差将（空气阻力不计）________ （填“增大”、“减小”、“不变”）．[1]

将一小球以初速度v从地面竖直上抛后，经4s小球离地面高度为6m，若要使小球抛出后经2s达相同高度，则初速度v₀应（g="10" m/s²，不计阻力） （    ）[2]

A．小于v	B．大于v
C．等于v	D．无法确定

竖直向上抛出一小球，3s末落回到抛出点，则小球在第2秒内的位移（不计空气阻力）是（    ）[1.5]

A．10m

B．0

C．-5m

D．-1.25m

竖直上抛的物体，在上升阶段的平均速度是20 m/s，则从抛出到落回抛出点所需时间为­______s，上升的最大高度为_______m．（g=10m/s²）[2]

如图2-18（原图2-25）所示的滑轮组，物体1、2分别具有向下的加速度a₁和a₂，物体3具有向上的加速度a₃，求a₁、a₂、a₃之间的关系．

图2-3（原图2-8）是在高速公路上用超声波测速仪测量车速的示意图，测速仪发出并接收超声波脉冲信号。根据发出和接收到的信号间的时间差，测出被测物体的速度。图2-4（原图2-9）中p₁、p₂是测速仪发出的超声波信号，n₁、n₂分别是p₁、p₂由汽车反射回来的信号．设测速仪匀速扫描，p₁、p₂之间的时间间隔△t = 1.0s，超声波在空气中传播的速度是v = 340m/s，若汽车是匀速运动的，则根据图2-9可知，汽车在接收到p₁、p₂两个信号之间的时间内前进的距离是__________m，汽车的速度是___________m/s． [8]

一辆汽车向悬崖匀速驶近时鸣喇叭，经t­₁=8s后听到来自悬崖的回声；再前进t₂=27s，第二次鸣喇叭，经t₃=6s又听到回声．已知声音在空气中的传播速度v₀=340m/s，求：
⑴汽车第一次鸣喇叭时与悬崖的距离；
⑵汽车的速度．[3 ]

天文观测表明，几乎所有远处的恒星（或星系）都以各自的速度背离我们而运动，离我们越远的星体，背离我们运动的速度（称为退行速度）越大；也就是说，宇宙在膨胀．不同星体的退行速度v和它们离我们的距离r成正比，即
v = Hr
式中H为一常量，已由天文观察测定．为解释上述现象，有人提出一种理论，认为宇宙是从一个大爆炸的火球开始形成的．假设大爆炸后各星体以不同的速度向外匀速运动，并设想我们就位于其中心，则速度大的星体现在离我们越远．这一结果与上述天文观测一致．
由上述理论和天文观测结果，可估算宇宙年龄T，其计算式为T ____________．根据过去观测，哈勃常数H = 3×10^－2m/s·l.y.，其中l.y.(光年)是光在1a(年)中行进的距离，由此估算宇宙的年龄约为__________________a．（1999年．上海卷）[6]

甲、乙、丙三辆汽车以相同的速度经过某一路标，以后甲车一直做匀速直线运动，乙车先加速后减速运动，丙车先减速后加速运动，它们经过下一路标时的速度又相同，则（  ）。[2 ]

A．甲车先通过下一个路标

B．乙车先通过下一个路标

C．丙车先通过下一个路标

D．三车同时到达下一个路标