2014年10月8日,月全食带来的“红月亮”亮相天空,引起人们对月球的关注。我国发射的“嫦娥三号”探月卫星在环月圆轨道绕行n圈所用时间为t,如图所示。已知月球半径为R,月球表面处重力加速度为g月,引力常量为G.试求:
(1)月球的质量M;
(2)月球的第一宇宙速度v1;
(3)“嫦娥三号”卫星离月球表面高度h.
如图所示,是发射嫦娥三号飞船登月的飞行轨道示意图,嫦娥三号飞船从地球上A处发射,经过地月转移轨道,进入环月圆形轨道,然后在环月圆形轨道上的B点变轨进入环月椭圆轨道,最后由环月椭圆轨道上的C点减速登陆月球,下列有关嫦娥三号飞船说法正确的是 ( )
| A.在地面出发点A附近,即刚发射阶段,飞船处于超重状态 |
| B.飞船的发射速度应大于11.2km/s |
| C.在环绕月球的圆轨道上B处须点火减速才能进入椭圆轨道 |
| D.在环月椭圆轨道上B点向C点运动的过程中机械能减小 |
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上P点,沿水平方向以初速度 抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球的半径为R.不考虑其它可能存在的阻力。求该星球上的第一宇宙速度
抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为α,已知该星球的半径为R.不考虑其它可能存在的阻力。求该星球上的第一宇宙速度
某载人飞船运行的轨道示意图如图所示,飞船先沿椭圆轨道1运行,近地点为Q,远地点为P。当飞船经过点P时点火加速,使飞船由椭圆轨道1转移到圆轨道2上运行,在圆轨道2上飞船运行周期约为90min。关于飞船的运行过程,下列说法中正确的是 
| A.飞船在轨道1和轨道2上运动时的机械能相等 |
| B.飞船在轨道1上运行经过P点的速度小于经过Q点的速度 |
| C.轨道2的半径小于地球同步卫星的轨道半径 |
| D.飞船在轨道1上运行经过P点的加速度等于在轨道2上运行经过P点的加速度 |
已知地球半径为R、自转周期为T、地面重力加速度为g。关于地球同步卫星,下列说法正确的是
A.地球同步卫星的轨道半径为 |
B.地球同步卫星的轨道半径为 |
C.地球同步卫星的运行速度与第一宇宙速度的比值为 |
D.地球同步卫星的运行速度与第一宇宙速度的比值为 |
如图所示,同步卫星与地心的距离为r,运行速率为v1,向心加速度为a1;地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则下列比值正确的是( )
A.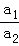 = =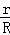 |
B.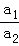 =( =( )2 )2 |
C.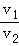 = =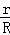 |
D.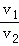 = = |
关于绕地球作匀速圆周运动的人造地球卫星和宇宙飞船,下列说法中错误的是( )
| A.若已知人造地球卫星的轨道半径和它的周期,利用引力常量,就可以算出地球质量 |
| B.两颗人造地球卫星,只要它们的绕行速率相等,不论它们的质量、形状是否相同,它们的绕行半径和绕行周期一定是相同的 |
| C.两颗人造卫星一前一后在同一轨道上沿同一方向绕行,若要后一卫星追上前面卫星并发生碰撞,只要将后者速率增大一些即可 |
| D.在绕地球飞行的宇宙飞船中,若宇航员从舱内慢慢走出,并离开飞船,此飞船的速率不会因质量减小而改变 |
研究表明,地球自转在逐渐改变,3亿年前地球自转的周期约为22小时。假设这种趋势会持续下去,且地球的质量、半径都不变,若干年后()
| A.近地卫星(以地球半径为轨道半径)的运行速度比现在大 |
| B.近地卫星(以地球半径为轨道半径)的向心加速度比现在小 |
| C.同步卫星的运行速度比现在小 |
| D.同步卫星的向心加速度与现在相同 |
北京时间2013年6月13日13时18分,天宫一号目标飞行器与神舟十号飞船成功实现自动交会对接(如图)。交会对接飞行过程分为远距离导引段、自主控制段、对接段、组合体飞行段和分离撤离段。则下列说法正确的是 ( )
| A.对接前,“神舟九号”欲追上“天宫一号”,必须在同一轨道上点火加速 |
| B.对接时,“神舟九号”与“天宫一号”所受万有引力的大小一定相等 |
| C.在组合体飞行段,神舟九号与天宫一号绕地球作匀速圆周运动的速度大于7.9km/s |
| D.分离后,“神舟九号”变轨降低至飞行轨道运行时,其动能比在交会对接轨道时大 |
甲、乙为两颗地球卫星,其中甲为地球同步卫星,乙的运行高度低于甲的运行高度,两卫星轨道均可视为圆轨道。以下判断正确的是( )
| A.甲的周期大于乙的周期 | B.甲的加速度大于乙的加速度 |
| C.乙的速度小于第一宇宙速度 | D.甲在运行时能经过北极的正上方 |
人造卫星绕地球做匀速圆周运动,设地球的半径为R,地面处的重力加速度为g,则人造卫星( )
A.绕行的最大线速度为 |
B.绕行的最小周期为 |
C.在距地面高为R处的绕行速度为 |
D.在距地面高为R处的周期为 |
在半径R=5 000 km的某星球表面,宇航员做了如下实验,实验装置如图甲所示.竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量m=0.2 kg的小球,从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙所示.求:
(1)圆轨道的半径及星球表面的重力加速度.
(2)该星球的第一宇宙速度.
宇航员在一个半径为R的星球上,以速度v0竖直上抛一个物体,经过t秒后物体落回原抛物点,如果宇航员想把这个物体沿星球表面水平抛出,而使它不再落回星球,则抛出速度至少应是 ( ).
A. |
B. |
C. |
D. |
已知一颗人造卫星在半径为R的某行星上空绕该行星做匀速圆周运动,经过时间t,卫星运动的弧长为s,卫星与行星的中心连线扫过的角度是θ弧度。(已知万有引力常量为G)求:
(1)人造卫星距该行量表面的高度h;
(2)该行量的质量M;
(3)该行量的第一宇宙速度v1。